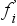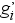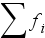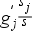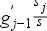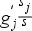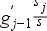Tartalom
- 1. Jelmagyarázat és rövidítésjegyzék
- 2. Bevezetés
- 3. Nagy mennyiségű adatok feldolgozásának statisztikai alapjai
- 4. Adatbázisok fellelhetősége az interneten
- 5. Adatbázisok használatának jogi háttere
- 6. Adatminőségi osztályok (adatok pontossága, adatok megbízhatósága)
- 7. Adatok előkészítése kiértékelésre (szűrés, normalizálás, u-próba, t-próba)
- 8. Környezetvédelem során mért adatok különleges feldolgozása
- 9. Adattárolási módok számítógépes feldolgozás során
- 10. Adatábrázolási technikák, mérési hibák vizuális ábrázolása, görbe és trendvonal illesztése adatsorokra
- 11. Nagy mennyiségű adatok kezelése és összehasonlítási módszerei
- 12. Adattrendek használatának lehetőségei a fenntartható fejlődés tervezésének támogatására
- 13. Ajánlott irodalom
- 14. Segédtáblázatok
Az ábrák listája
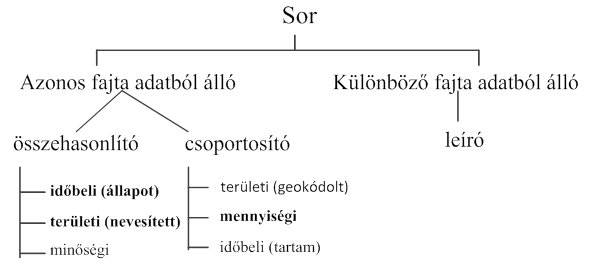
- 3.1. Statisztikai sorok fajtái (vastagon kiemelve a leggyakoribb előfordulás)
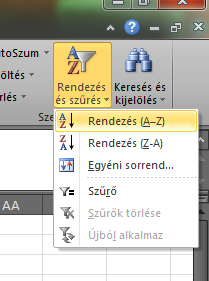
- 3.2. Adatok rendezésének gombja MS Excelben
- 3.3. Adatok rendezésének gombja LibreOfficeban
- 3.4. Módusz kiemelése a sokaságból
- 3.5. Vizsgált adatsor jellemzői számegyenesen
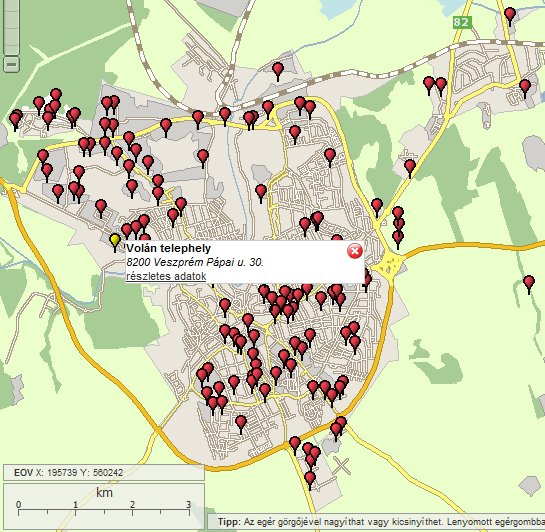
- 4.1. Veszprém levegőt terhelő pontforrásai
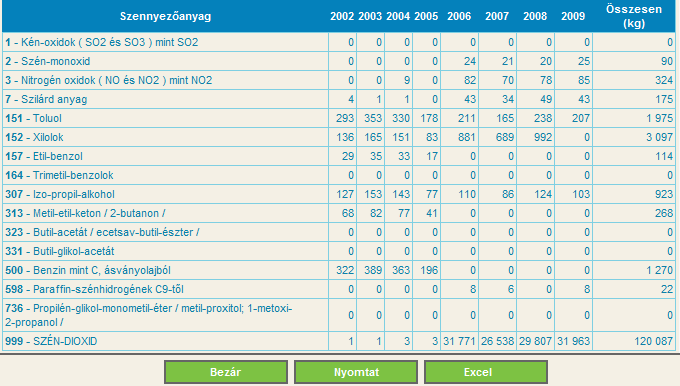
- 4.2. Volán telephely éves szennyezőanyag kibocsátása (kg)
- 4.3. Veszprém – Kádár utcai mérőkonténer adatlapja
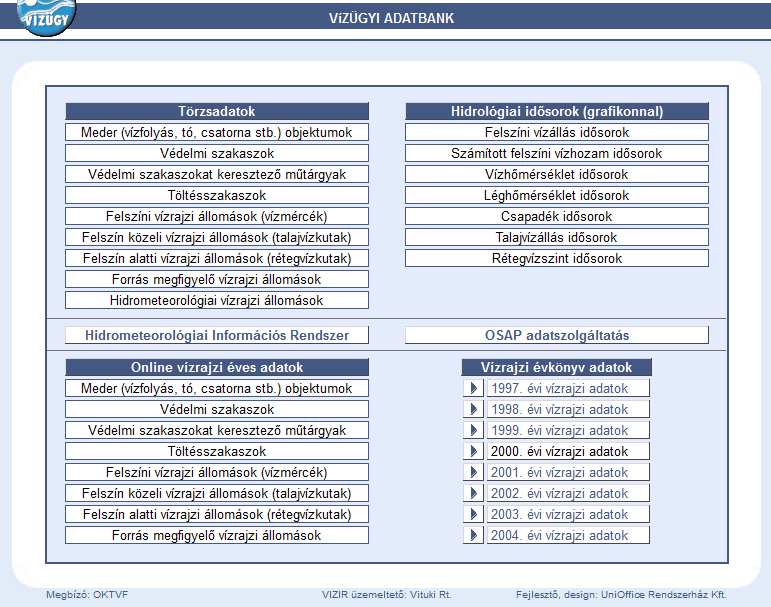
- 4.4. Vízügyi adatbank kezdőlapja
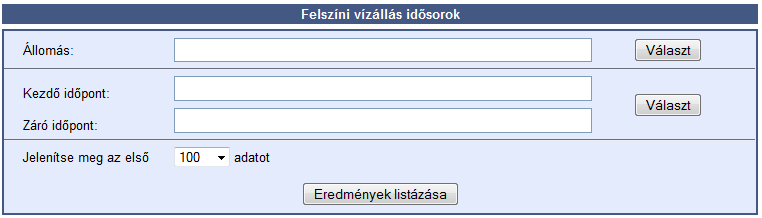
- 4.5. Vízügyi adatbank lekérdező felülete
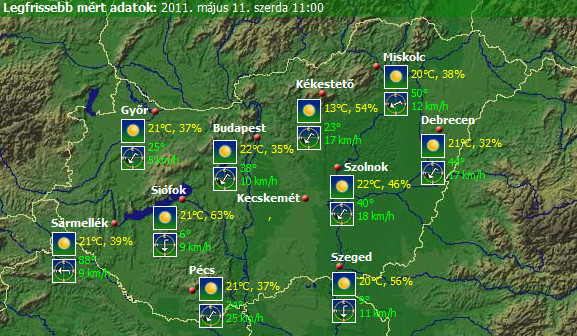
- 4.6. Met.hu legfrissebb mért meteorológiai adatai
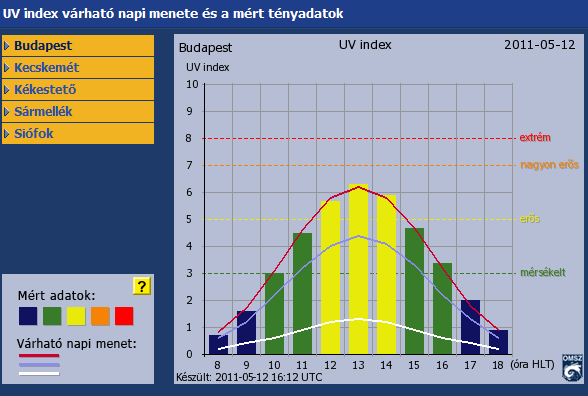
- 4.7. UV index várható napi menete
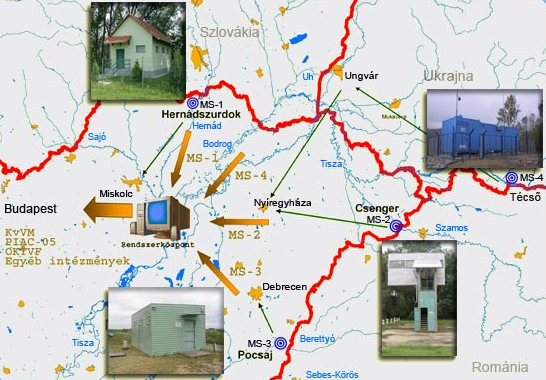
- 4.8. Tisza-vízgyűjtő monitoring rendszer
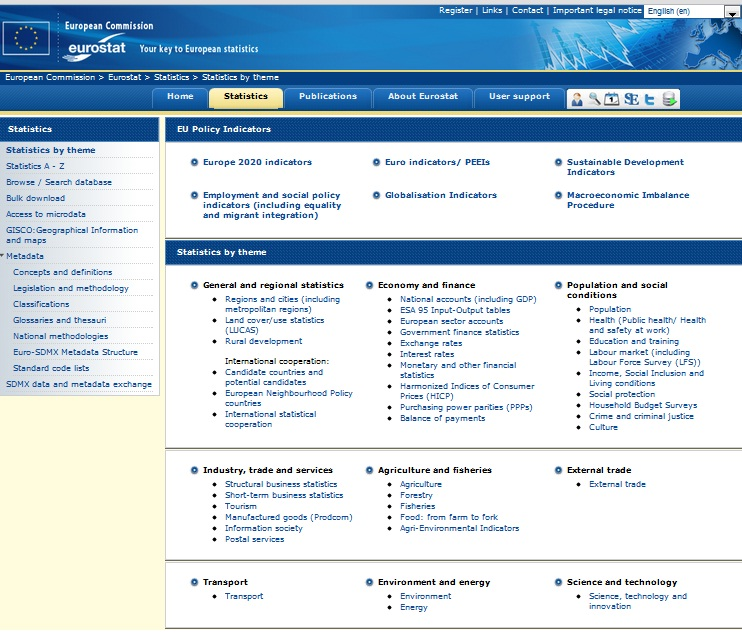
- 4.9. Európai Statisztikai Hivatal témakörei
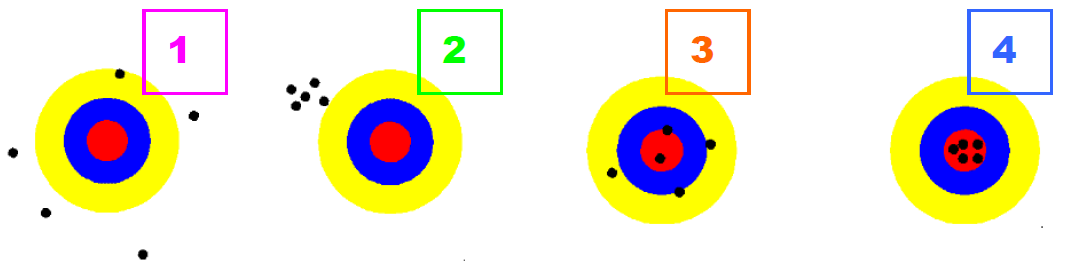
- 6.1. A kezdő és a pontosan célzó „találatai”
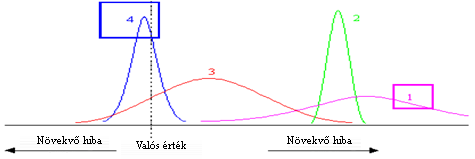
- 6.2. A kezdő és a pontosan célzó „találatai”- szóródási görbe
- 6.3. Szisztematikus hiba – torzítás illusztrációja
- 6.4. Véletlen hiba – szórás/pontosság illusztrációja
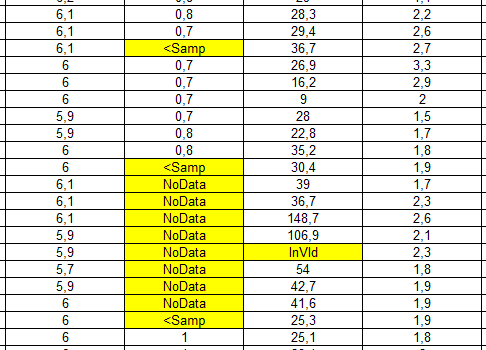
- 7.1. Probléma az adatbázisban
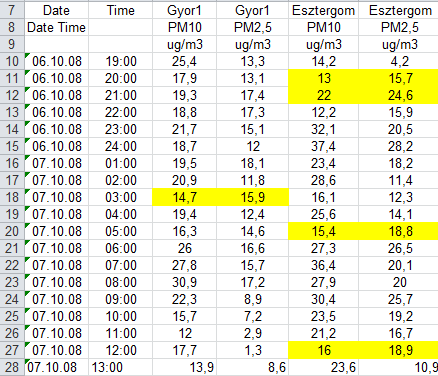
- 7.2. ÉDT-KTVF adatbázisából részlet
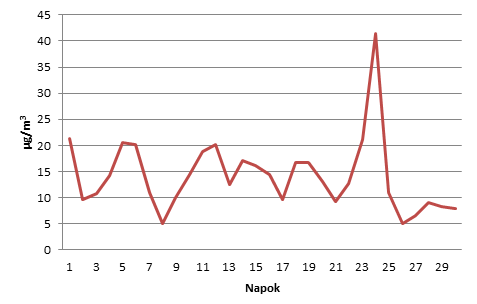
- 7.3. SO2 koncentráció változása a mintahónapban
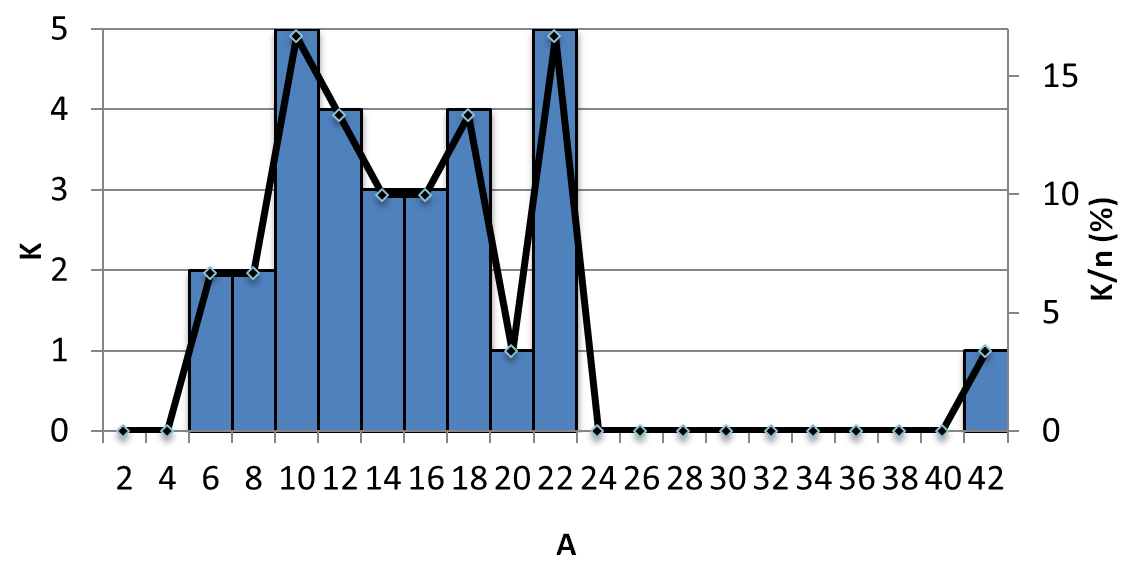
- 7.4. SO2 tartalom relatív gyakorisági eloszlása
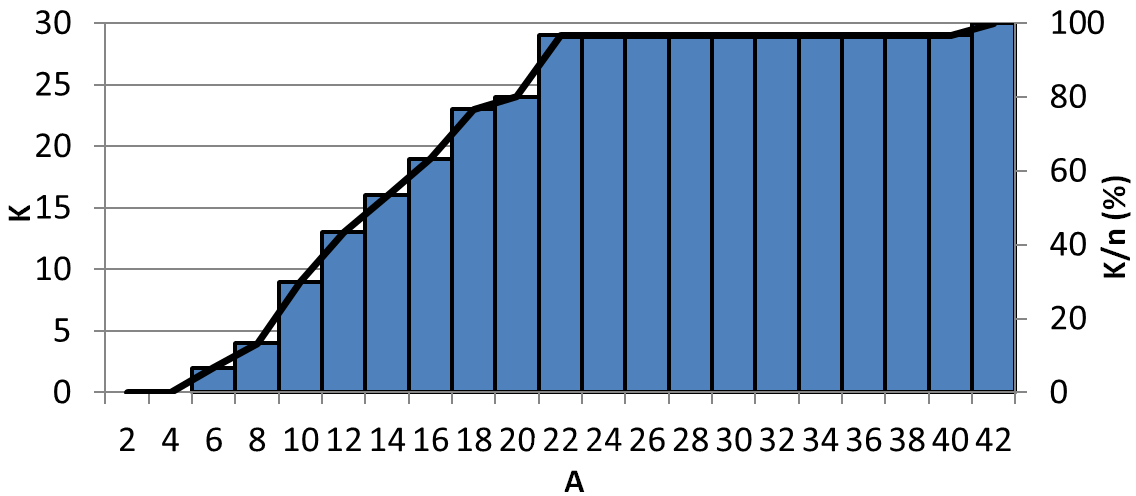
- 7.5. SO2 összegzett relatív gyakorisági eloszlása
- 7.6. Párhuzamos mérési helyszínek - Veszprém
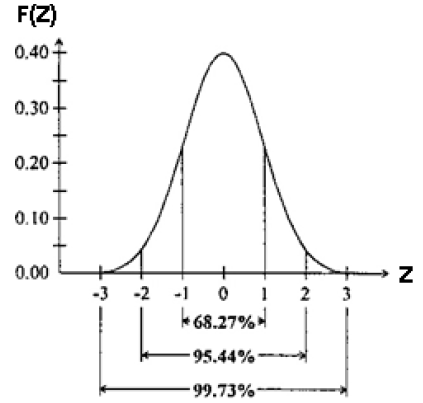
- 7.7. A standard normáleloszlás sűrűségfüggvénye
- 8.1. Nagytérfogat-áramú pormintavevő, és a szűrőpapíron felfogott porminta
- 9.1. A hardver, szoftver és az adat árainak egymáshoz viszonyított aránya a számítástechnika korai korszakában és ma
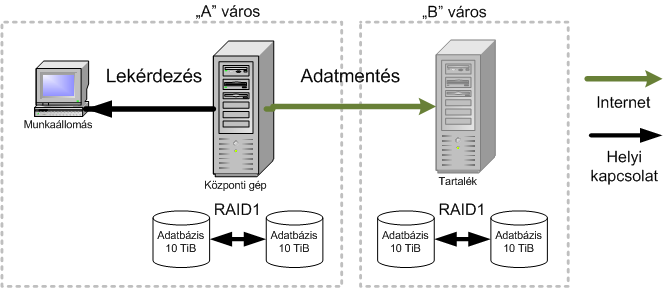
- 9.2. Klasszikus – adatbiztonságra kiépített – adatbázis hardver környezet
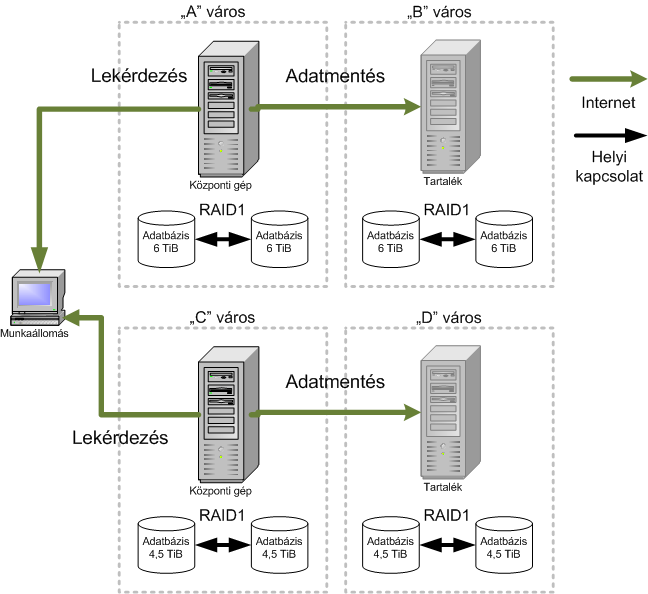
- 9.3. Osztott – adatbiztonságra kiépített – adatbázis hardver környezet
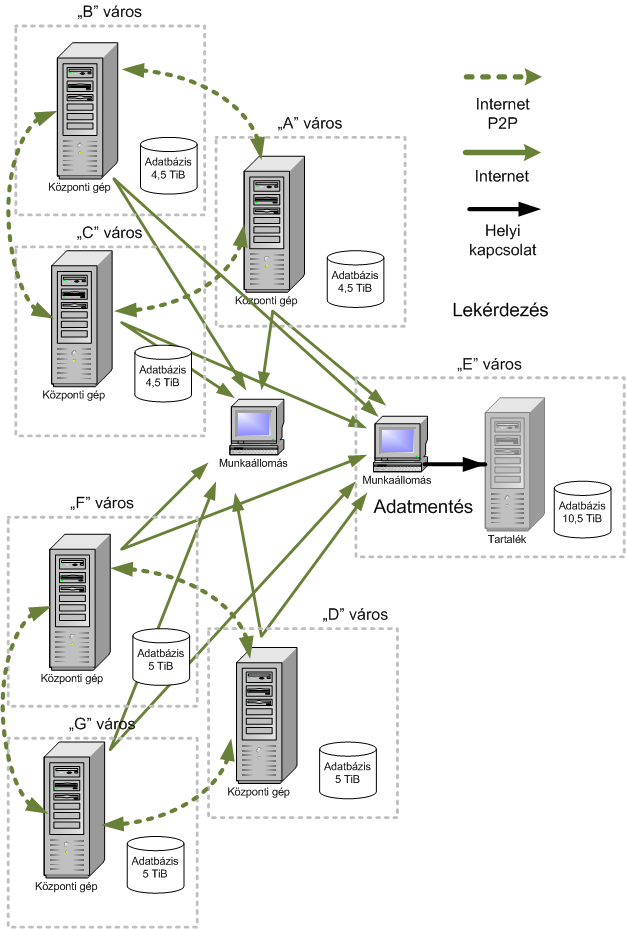
- 9.4. Korszerű – adatbiztonságra kiépített – adatbázis hardver környezet
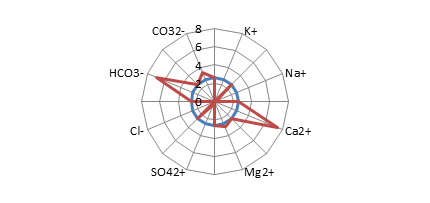
- 10.1. Összes só-tartalom csillagábra
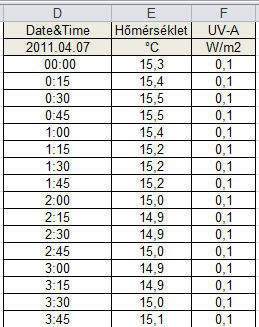
- 10.2. Példaként bemutatott 9.3 diagramjának adatsora – részlet a 24 órás mérés eredményeiből
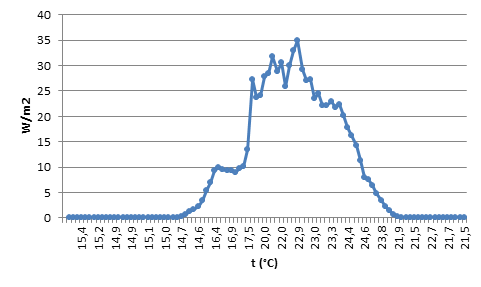
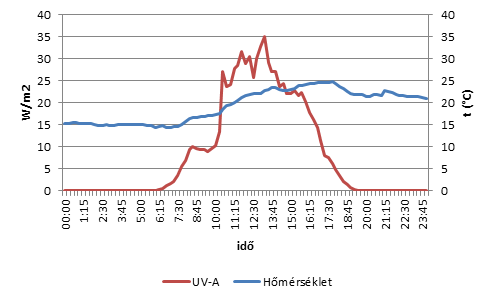
- 10.3. Hőmérséklet – UVA sugárzás pont (felső)- illetve vonaldiagramon (alsó)
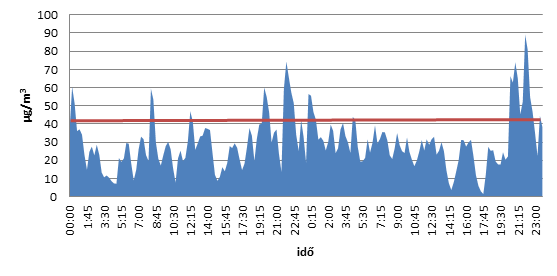
- 10.4. 2010. október 8-9. – Devecseri mérésünk PM10 koncentráció értékei és a határérték
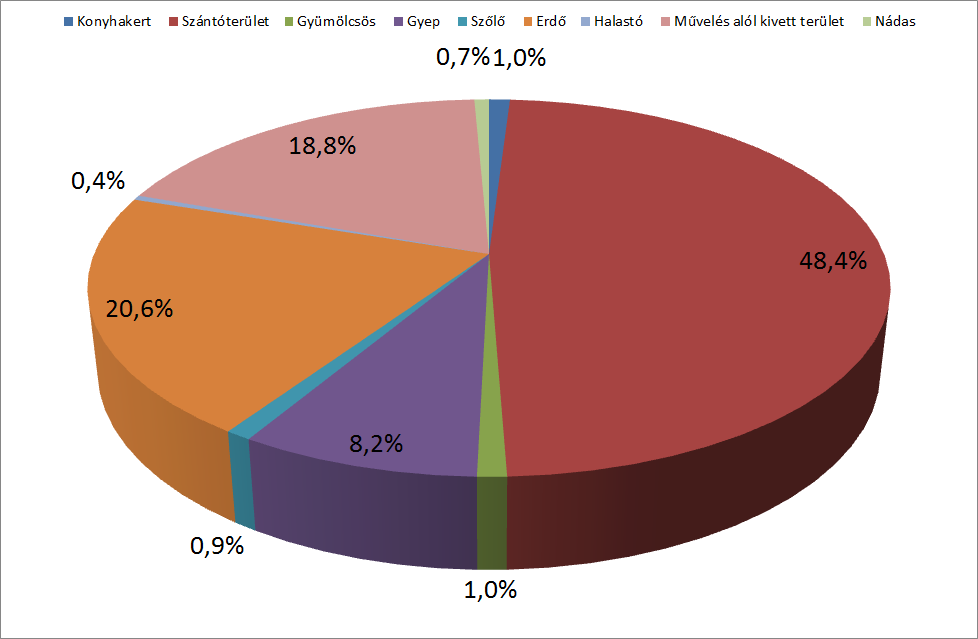
- 10.5. Földhasználat művelési ágak szerint (2010) – KSH adatai szerint
- 10.6. Földhasználat művelési ágak szerint (2010-külső perec, 2008-belső perec) – KSH adatai szerint
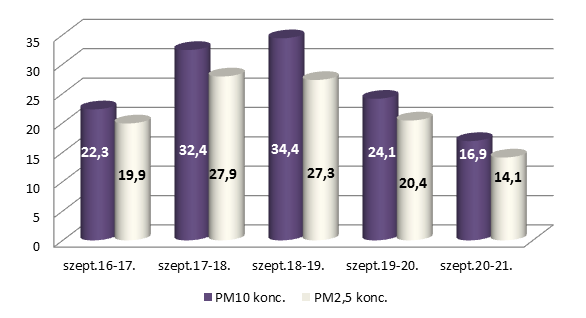
- 10.7. Balaton Pláza – egyidejűleg mért PM10/PM2,5 szálló por frakciók koncentráció értékei
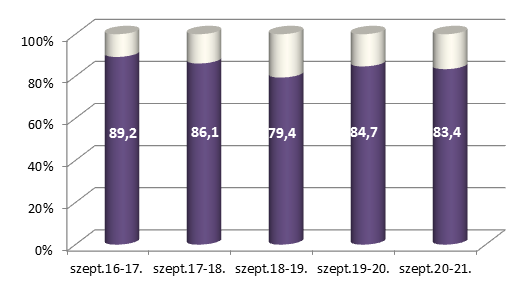
- 10.8. Balaton Pláza – PM2,5 frakció aránya a PM10 koncentrációban
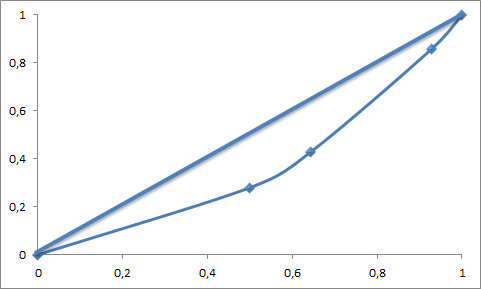
- 11.1. Lorenz görbe.
- 12.1. Várpalota, Inota, Pétfürdő – NO2 koncentrációk éves átlagértékeinek változása 1979-2008 között
- 12.2. Várpalota, Pétfürdő – SO2 koncentrációk éves átlagértékeinek változása 1979-2008 között
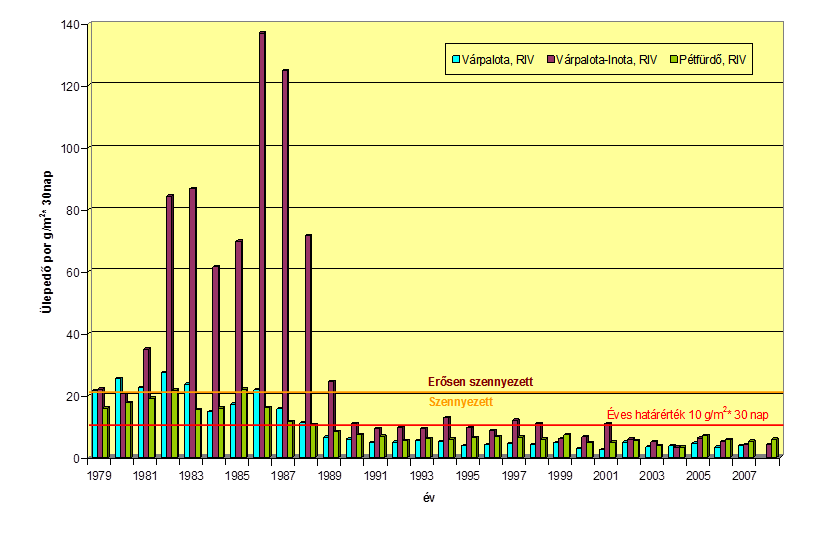
- 12.3. Várpalota, Inota, Pétfürdő – Ülepedő por koncentrációk éves átlagértékeinek változása 1979-2008 között
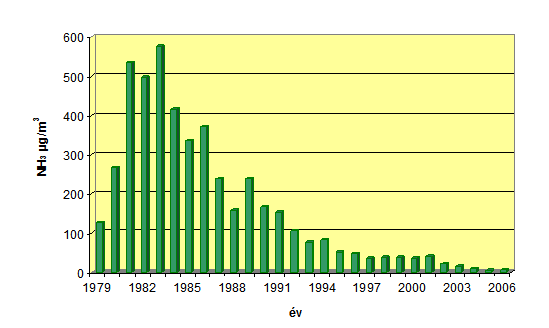
- 12.4. Pétfürdő – Ammónia koncentrációk éves átlagértékeinek változása 1979-2006 között
A táblázatok listája
- 3.1. Megoszlási viszonyszám számítása táblázatkezelő rendszerben
- 3.2. Szmogriadók száma 2008-2011 között
- 3.3. Osztályközös gyakoriság alaptáblázata
- 3.4. Veszprémi légszennyezettség-mérő állomás órás NOx töménység-mérési adatai
- 3.5. Osztályköz táblázat egyenletes osztályköz esetén
- 3.6. Kumulált gyakoriság
- 3.7. Felfelé kumulált gyakoriság számítása
- 3.8. Lefelé kumulált gyakoriság számítása
- 3.9. Relatív kumulált gyakoriság
- 3.10. Mérőcsoportok
- 3.11. Értékösszegsor számítása.
- 3.12. Kvantilisek.
- 3.13. Kvantilisek meghatározásához kiindulási adattábla.
- 3.14. Medián számítás alapadatai felfelé kumulált gyakorisággal
- 3.15. Medián számítás alapadatai relatív kumulált gyakorisággal
- 3.16. Módusz meghatározásának lépései
- 3.17. Módusz meghatározása makróval.
- 3.18. Terjedelem meghatározása.
- 3.19. Szórás meghatározása.
- 3.20. Súlyozott szórás meghatározása.
- 3.21. Relatív szóródás meghatározása.
- 3.22. Különbség számításához alapadatok
- 3.23. Momentum számítás (berendezés megbízhatósága)
- 4.1. Monitorállomások alap-műszerezettsége
- 7.1. Hibaszámítási adatok – feladat megoldása
- 7.2. Egymintás t- próba – feladat megoldása
- 7.3. A feladat megoldása – 1. rész
- 7.4. A feladat megoldása – 2. rész
- 7.5. PM10 - párhuzamos mérések eredményei
- 7.6. PM2,5 - párhuzamos mérések eredményei
- 7.7. Statisztikai vizsgálatok eredménye
- 7.8. Feladat megoldása standardizálással
- 10.1. Vizsgált mintavételi helyre jellemző összessó-tartalom jellemző és számított adatsorai
- 11.1. Szennyvízkibocsátók az ipari parkban.
- 11.2. Előzetes számítások a Gini-együtthatóhoz.
- 11.3. Osztályközök létrehozása.
- 11.4. Gyakoriságok értékei.
- 11.5. Gyakoriságok számítása.
- 11.6. Érkékösszegsorok.
- 11.7. Értékösszegsorok számítási módja.
- 11.8. Gini együtthatóhoz szükséges segédtábla
- 11.9. Gini együtthatóhoz szükséges segédszámítások.
|
dB |
deciBell, a hangnyomásszint mértékegysége |
|
WGS84 |
A GPS által használt vonatkoztatási rendszer |
|
GPS |
global positioning system (globális helymeghatározó rendszer) |
|
EOV |
egységes országos vetület |
|
b |
kiindulási (bázis) érték jelölése |
|
bi |
bázis-viszonyszám értéke az i. adatra |
|
y |
statisztikai adat illetve egyed (elemi információegység) |
|
yi |
az i. adat |
|
li |
lánc-viszonyszám értéke az i. adatra |
|
Vm |
megoszlási viszonyszám |
|
n |
elemek száma |
|
Vi |
intenzitási viszonyszám |
|
fi |
abszolút gyakoriság |
|
gi |
relatív gyakoriság |
|
xi |
osztályközép értéke |
|
Yi0 |
az i. osztályköz alsó határértéke |
|
Yi1 |
az i. osztályköz felső határértéke |
|
hi |
hosszúsága |
|
k |
osztályközök száma |
|
|
abszolút kumulált gyakoriság |
|
|
relatív kumulált gyakoriság |
MIÉRT FONTOS AZ ADATKEZELÉS?
Jelen jegyzet a leendő fenntartható fejlődés szakértő hallgatók számára a szükséges részletességig ismerteti az adatgyűjtés és –értékelés matematikai hátterére, ugyanakkor a fenntartható fejlődés témaköréből választja a példákat, és azokon keresztül mutatja be adatok felhasználásának módját és lehetőségeit.
A környezetvédelmi elemzések során rendszerint hatalmas mennyiségű – jellemzően – számadat keletkezik. Az emberi agy felépítéséből következően inkább analitikus, elemző munkára képes, mint manuális, monoton számítások elvégzésére. e összhangot kell találni az emberi gondolkodás és a gépi számítások között. Ebben szintén segítséget nyújt e könyv, bemutatva mit lehet a gépre bízni és mi az amit emberi elmére.
A jegyzet elektronikus tanulásra készült és feltételezi, hogy megfelelő számítógépes alapismeretekkel rendelkezik a felhasználó a példák LibreOffice (régebben OpenOffice) Calc vagy Microsoft Office Excel szoftveren történő gyakorlására. Az anyag megértéséhez – mivel bármilyen felsőfokú végzettséggel rendelkező hallgató számára érthető kíván maradni – csak alapvető matematikai ismeretekkel kell rendelkezni. Éppen ezért az anyag egy része a mérnök és gazdálkodás szakon végzettek számára már ismert lehet, de a példák környezetvédelmi vonatkozásai miatt nekik is célszerű átolvasni e részeket.
A digitális technológia kiszélesíti a tanulási lehetőségeket, és egyben meg is változtatja a tanítási módszereket. Az elektronikus tananyagoknak mindenekelőtt felhasználóbarátnak kell lenniük, hiszen ha nem élvezetes a velük való foglalkozás az elveheti a hallgatók kedvét a tanulástól, az adott témától, anyagrésztől.
Az anyagból meg fogjuk ismerni az adatokkal való dolgozás buktatóit és hogyan vehetjük észre e csapdákat. Megismerjük, hogyan lehet ugyanabból a hiteles mérési adatsorból kiindulva „bizonyítani”, hogy a légszennyezés egy településen 50%-kal nőtt és azt is, hogy 30%-kal csökkent; és azt is hogyan lehet az ilyen típusú adatfeldolgozásokat felismerni.
Tartalom
A világunkat a számok mozgatják. Mégis egyre többen vannak, akik idegenkednek a számok világától és nem értik vagy nem akarják érteni azok jelentését. A természet és a világgazdaság folyamatainak megértéséhez elengedhetetlenül szükséges a számok elemzésének ismerete, a statisztika. E fejezet célja, hogy közérthetően, példákkal szemléltetve megismertesse az olvasóját a statisztika alapjaival. Nem célja, hogy statisztikusokat képezzen, ezért csak szemezget a mindennapi életben leggyakrabban előforduló ismeretekből. Ezen ismeretekkel könnyebben kivédhetjük azt a – sajnos – egyre gyakoribb tapasztalatot, hogy mind több és több gazdasági és politikai szereplő kihasználja az emberek statisztikai hiányosságait. Ez legtöbbször abban nyilvánul meg, hogy olyan összefüggéseket hitetnek el velünk, amilyeneket – ha nem a számok nyelvén mondanák – senki nem hinne el.
Mi is a statisztika? A következő két megfogalmazás két híres magyartól származik:
Lukács Ottó: „Tapasztalati adatokból (mintákból) következtetni az egész sokaság valószínűségeire, eloszlás- és sűrűségfüggvényeire, azok paramétereire.”
-
Besenyei Lajos: „A valóság tényeinek tömegét tömören, a számok nyelvén jellemző tudományos módszertan illetve gyakorlati tevékenység.”
Mindkét állítás jól leírja a lényeget, de Besenyei megfogalmazása közelebb áll a környezetvédelemmel, a fenntartható jövővel foglalkozó szakemberek munkájához. Az adatokkal való munka során célunk a valóság folyamatainak elemzése, amit legtöbbször a jövőre vonatkozó becslések követnek. Ahhoz, hogy megértsük, a statisztika alapjait néhány fogalmat tisztázni kell:
-
Sokaság (populáció): A vizsgálat (megfigyelés) tárgyát alkotó egyedek összessége. Napjainkban egyre többször azonosítjuk az adat megnevezéssel. Ezen irányzat a számítástechnika előretörésével egyre inkább terjed.
-
Megfigyelési egység: amelyre/akire a megfigyelés irányul
-
Számbavételi egység: amely/aki információt szolgáltat a megfigyelési egységre vonatkozóan
Az adatokkal való munka egyik kulcslépése, hogy képesek legyünk besorolni az adatunkat a megfelelő sokasági kategóriákba. E kategóriák a következő képen oszthatóak fel:
-
Vonatkozás szerint
Időpontra: Egy jól meghatározható időpontra (tegnap, tavaly, 1974.09.01-én, stb).
Időtartamra: Két időpont között (hétfőtől péntekig, 1974-2000-ig). De például tavaly január 1-től december 31-ig szintén időtartam, bár megegyezik az időpontban példaként felsorolt „tavaly” fogalommal. A különbség: itt a 365 darab napot értjük rajta, míg az időpontnál a teljes évet, mint „év” vesszük figyelembe.
-
Érték szerint
Diszkrét: Ide tartoznak, azok az adatok, amelyek már nem változnak meg az idő előrehaladtával. Időpontra és időtartamra is vonatkozhat. Például a települések száma egy adott időpontban vagy a tavalyi évben (időtartam) bejelentett szmog-riadók száma egy településen.
Folytonos: Ezen adatoknál csak az adott pillanatig bekövetkezett eseményeket tudjuk számszerűsíteni, amely akár már a következő időpillanatban megváltozhat. Vonatkozhat időpontra és időtartamra is. Például: szmogos napok száma idén (időtartam) vagy jelenleg belvízzel borított területek mérete (időpont).
-
Típusra:
Álló (állomány): Ebben az esetben a sokaság egy darab jó meghatározható értékből áll, ami önmagában is értelmezhető. Csak időpontra vonatkozhat. Például a talaj-közeli ózon napi átlagos töménysége tegnap (időtartam esetén) vagy talaj-közeli ózon jelenlegi átlagos töménysége (időpont esetén).
Mozgó (áramlás): E típus esetén egy adattömeggel dolgozunk, amely azonos jelenségnek írja le az időbeni változását. Csak időtartamra vonatkozhat. Például a talaj-közeli ózon óránkénti átlagos töménysége (időtartam).
A sokasági kategóriába történő besorolást nagy mértékben segíti ha pontosan utánajárunk az adatok forrásának és jelentésének. E megállapítás bár köznapinak tűnik, nem szabad könnyelműen kezelni: nagyon sokszor még a gyakorlott tudósok is gondban vannak egy adat jelentésének megállapításánál. Ennek oka, hogy számos adatközlő nem tájékoztat arról, hogy pontosan mit is takar az adott adat (hogyan mérték, milyen pontosságú a műszer, stb.).
Az ismérv a sokaság egységeit jellemző tulajdonság vagy az adott szempont szerint lehetséges tulajdonságok halmaza. Gyakorlatilag olyan szempontok, amelyek alapján a sokaság egymást át nem fedő részekre bontható.
Az egyes ismérvkategóriákra adható válaszok az ismérvváltozatok, amelyek lehetnek megszámlálhatóak (például a kémhatás csak savas, lúgos vagy semleges lehet, de a NOX töménység értéke – majdnem – bármilyen nagy szám lehet és csak a mérés pontosság határozza meg, hogy hány változata fordulhat elő). Azoknál az ismérvváltozatoknál, ahol csak két változat van, alternatív ismérvnek is hívjuk. A mennyiségi ismérvek ismérvváltozatait ismérvértéknek is nevezhetőek.
Az ismérveket több féle képen csoportosíthatjuk. Fő csoportosítás alapján lehet
-
közös (a sokaság minden tagjára igazak) vagy
-
megkülönböztető (az egyedek vagy azok egy csoportja elkülöníthető).
Ezen kívül jellemzőjük alapján négy csoportba soroljuk az ismérveket:
-
Tárgyi ismérvek
Minőségi ismérv: A sokaság számszakilag, időponttal vagy térbeli adattal ki nem fejezhető (jellemzően azonosításukat szolgáló) ismérvei. Ilyen ismérv például a légszennyező anyag, ismérvváltozatai az NOX, O3, CO2, stb.para>
Mennyiségi: A sokaság számokkal kifejezhető (mérhető) egyedei. A statisztika ezen ismérvekkel foglalkozik a leggyakrabban. Ilyen ismérv például a föld-közeli ózon töménysége.
-
Időbeli ismérv: A sokaság adott elemének időpontját tároló érték. Értéke lehet egy pontos időpont, de lehet időtartam is. Például a mérés ideje (időpont) vagy a mérés időtartama.
-
Területi ismérv: A sokaság adott elemének földrajzi rögzítésére szolgáló ismérv. Lehet számszerűsített (például a mérés GPS koordinátája), közismert nevekhez kötött (például Veszprém) vagy viszonylagos (például „a második emeleten”).
Mérésnek az egységek számokkal való jellemzését értjük. A környezetvédelemben négy mérési skálát (szintet) használunk.
-
Nominális (névleges) mérési skála: Az egységekhez rendelt számértékek egyező vagy különböző voltát engedi meg. Például:
Két talajminta higany töménysége azonos-e vagy sem. (Figyeljük meg a példát: az információból nem tudjuk magasabb-e, vagy alacsonyabb a higany töménysége, sem egyéb ismeretet.)
Van-e higany a talajban vagy nincs.
-
Ordinális (sorrendi) mérési skála: Az egységek a tulajdonságok szerint rangsorba állíthatók. (Tudunk nagysági különbséget tenni közöttük. Tudjuk, hogy nagyobb, kisebb, de a mértékét nem.). Például:
A talajminta higanytartalma alapján milyen szennyezettség-osztályba tartozik. (De nem tudjuk – vagy nem érdekes – az osztályok közötti pontos koncentráció-különbség.)
A mérési adatok higanytartalom szerinti sorrendje. Ez esetben nem ismert az adatok közötti távolság.
-
Intervallum mérési skála: A rangsorba rendezett tulajdonságokat egyenlő közök választják el, de nem tudjuk a kezdőértéket. Figyeljünk rá, hogy a „0” is köznek számít! Például:
A minta a 0-10 μg/kg, 10-20 μg/kg közötti higany töménységű talajok csoportjába tartozik-e? (De nem mondhatjuk, hogy a 20 μg/kg töménységű talaj kétszer szennyezettebb, mint a 10 μg/kg-os, mivel nem tudjuk mennyi a „tiszta” talaj higanytartalma.)
-
Arányskála: A kezdőpont egyértelműen adott és rögzített, s így a skálaértékek egymáshoz való aránya is meghatározható. Ezen skálába tartozó adatok valók teljes elemzési műveletek elvégzésére. Példa:
Tudjuk, hogy mennyi a talaj általános higany koncentrációja.
Fontos, hogy a besorolásoknál nem az számít, hogy mi az adat tényleges információtartalma, hanem, hogy milyen információ érdekes számunkra. Például egy éjszakai szórakozóhely hangnyomásszintjének („zajosságának”) felmérése során percenként rögzítjük öt ponton, egy-egy órán keresztül a hangnyomásszinteket. Ez az adatsor nominális skálának számít, ha csak arra vagyunk kíváncsiak, hogy átlépte-e a megengedett hangnyomásszintet a létesítmény, vagy sem. Ugyan ez az adatsor ordinális skálának minősül, ha arra vagyunk kíváncsiak, hogy a hangnyomásszint milyen súlyos a zajszennyezés (nincs büntetés, pénzbüntetés, bezárás). Végül lehet intervallum vagy arányskála is, ha a mérési adatokat 10 dB-ként csoportosítjuk és tudjuk a hallásküszöb értékét is.
A sokaság egységeinek bizonyos ismérvek szerinti csoportosítása, rendezése.
A benne szereplő adatok összegezhetősége szerint lehet:
-
Csoportosító statisztikai sor: adatai összegezhetők, számszakilag értelmezhetők (például árvízzel borított területek összes felülete).
-
Összehasonlító sor: adatai nem összegezhetők, számszakilag értelmetlen (például a minta színe)
A sorban szereplő adatok fajtái szerint:
-
idősor: időbeli ismérv alapján csoportosítva az adatokat
állapot idősor: Adatai számszakilag nem összegezhetők, egy adott időpontra vonatkoznak (például a mérés időpontja 2011.12.20. 08:15).
tartam idősor: Adatai számszakilag összegezhetőek (de nem felétlenül értelmesek is az összegzés után!), adatai időtartamra vonatkoznak (például az egymás követő mérések időtartama).
-
minőségi sor: Az adatoknak minőségi ismérv szerinti rendezése (például a minta szaga).
-
mennyiségi sor: Az adatoknak mennyiségi ismérv szerinti rendezése (például a hangnyomásszint mért értéke).
-
területi sor: Az adatok területi hovatartozást jelentenek.
nevesített területi sor: A területi adatok nem számszerűsített formában állnak rendelkezésre. Ilyen adat például: „a mérés a gyárkapu előtt történt”.
geokódolt területi sor: A területi adatok számszerűsített (geokódolt) formában állnak rendelkezésre, amelyekkel térbeli műveletek végezhetőek (például vektorműveletek). Ilyen adat jellemzően WGS84 („GPS”) vagy EOV koordináta.
-
leíró sor: Ebbe a kategóriába azok a sorok tartoznak, ahol egy mérés különböző tulajdonságát soroljuk fel. Jellemzően ezek az adatok a „megjegyzés” rovatban szoktak feltüntetésre kerülni egy mérés során.
Amikor két adatot vagy adatcsoportot szeretnénk összehasonlítani, akkor két vizsgált érték hányadosát statisztikai viszonyszámnak nevezzük. Az általunk érintett témakörben három viszonyszámot használunk nagy gyakorisággal:
-
Összehasonlító sorból: összehasonlítási viszonyszám (dinamikus, területi)
-
Csoportosító sorból: megoszlási viszonyszám
-
Leíró sorból: intenzitási viszonyszám számítható.
Két időszak adatának hányadosa. Csak idősorokból lehet számítani, a számított eredmény az idősor két adatának egymáshoz való aránya. A két adatot tárgy időszaknak (időben a vizsgálat céljához közelebbi adat) és bázis időszaknak (időben a vizsgálat céljától távolabbi adat)
Ha több időszakunk van (például egy év napi átlagos hőmérséklet adatai), akkor az viszonyíthatjuk egymáshoz (láncviszonyszám), vagy az időben első adathoz, amit bázisnak nevezünk (bázisviszonyszám). Számításuk a következő:
Bázis-viszonyszám: bi = yi / yb
Láncviszonyszám: li = yi / yi-1
A két viszonyszám egymásból is számítható a következő képletekkel:
Bázisviszonyszámból láncviszonyszám:
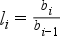
Láncviszonyszámból bázisviszonyszám:
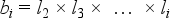
Egy adott sokaságból egy kiválasztott tartomány része. Értéke megmutatja, hogy a sokaságban milyen súllyal találhatók az adott csoport tagjai. Ezt a viszonyszámot használjuk leggyakrabban, ha valamilyen esemény előfordulásának gyakoriságára vagyunk kíváncsiak.
Számítása:
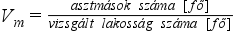
vagy
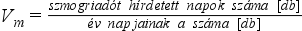
Számítása táblázatkezelő rendszerben:
3.1. táblázat - Megoszlási viszonyszám számítása táblázatkezelő rendszerben
A |
B | |
|---|---|---|
|
1 |
Minta azonosítója |
Szennyezett? |
|
2 |
AD231 |
igen |
|
3 |
AB322 |
nem |
|
4 |
AS231 |
nem |
|
5 |
AB343 |
nem |
|
6 |
AA231 |
igen |
|
7 |
Megoszlási viszonyszám a szennyezett mintára: |
KÉPLET* |
*ahol a képlet helyére a következőt kell írni, MS Office és LibreOffice esetében egyaránt:
=DARABTELI(B2:B6;"igen")/DARAB2(B2:B6)
Egy adott sokaság egészéből (pl. városok) egy másik sokaság egészére (pl. lakosság) mennyi jut. Célja, hogy meghatározhatjuk a sokaság egyedeit érő átlagos terhelést vagy megoszlást. (Ne keverjük össze a MEGOSZLÁSSAL!)
Számítása:
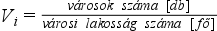
vagy
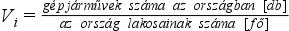
A számítás során az osztóban szereplő adatot a statisztikai gyakorlat – a könnyebb kezelhetőség érdekében - sok esetben nagyobb egységként veszi figyelembe. Például a második számítási minta esetében sokkal gyakoribb, hogy az osztó nem fő, hanem ezer fő. Ezzel egynél nagyobb számot tudunk kapni, amit könnyebben értelmezünk.
Egy vizsgáljuk meg, hogyan alakul a szmog-riadót hirdetett napok száma egy településen. Az adatok a következőek:
3.2. táblázat - Szmogriadók száma 2008-2011 között
|
Év |
Szmog-riadók száma (nap) |
|---|---|
|
2008 |
3 |
|
2009 |
6 |
|
2010 |
8 |
|
2011 |
5 |
Számítsuk ki a 2008-hoz, mint bázisévhez viszonyítva 2011 viszonyszámát:
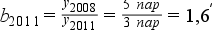
Számítsuk ki 2011 láncviszonyszámát 2010-es évhez képest:
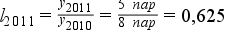
Mit olvashatunk ki a számokból? Ha 2011-et vizsgáljuk, akkor írhatunk egy újságcikket, amiben megállapíthatjuk – és számszakilag bizonyíthatjuk is –, hogy a szmog-riadós napok száma több mint másfélszeresére nőtt (bázisviszonyszám) de írhatunk olyat is, hogy a szmog-riadós napok száma több mint harmadával csökkent (láncviszonyszám). Ezen egyszerű példa is jól megvilágítja, hogy a statisztika kétélű tudományos módszer, amellyel szándékosan vissza lehet élni, de tudatlanságunkból fakadóan akaratlanul is félrevezethetjük magunkat és másokat.
Ahhoz, hogy az ilyen félreértelmezéseket elkerüljük:
-
Mindig tisztába kell lennünk az adatok forrásával: sok vizsgálat esetében attól függően, hogy milyen szabvány, milyen metódus szerint végezzük a mérést máshogy és máshogy értelmezendő adatokat kapunk. Kiemelten igaz ez a nagy léptékű társadalmi és gazdasági események mérésére, ahol nem homogén és nagyon nagy méretű a minta, ezért csak (reprezentatív) mintavétellel lehet mérni.
-
Lehetőleg az adatoknak a környezetét is ismerjük meg. Mint azt előző példafeladat alapján is látjuk, ha csak két adatot ismerünk, akkor nagyon könnyen belefuthatunk a folyamat egészére nem jellemző rendellenességbe, mérési hibába, váratlan eseménybe.
-
Értelmezzük az eredményt! Például ha csak annyit olvasunk, hogy a viszonyszám nézzük meg lánc- vagy bázisviszonyszám-e. Ha az olvassuk „arány”, akkor nézzük meg minek is az aránya? Egyáltalán összehasonlítható a két adat? Mialatt ezeket a kérdéseket feltesszük magunkban és megkeressük rá a választ az esetek döntő hányadában megbizonyosodhatunk arról, hogy megfelelően feldolgozott adattal van-e dolgunk.
A környezetvédelemben és általában a természettudományokban nagy szerep jut az empirikus eloszlásoknak. Amely a megfigyelések (kísérletek) eredményeként kapott adatok eloszlását jelenti. Amikor nem – csak – valós megfigyelések eredményeiről van szó, azt elméleti elosztásnak nevezzük és a valószínűség-számítás tárgykörébe tartozik.
Az eloszlás elemzés legfontosabb eszközei a következők:
-
Gyakorisági sorok
-
Kvantilisek
-
Középértékek
-
Szóródás
Valamely sokaságnak egy mennyiségi ismérv szerinti csoportosítása. Segítségével különösen a nagy mennyiségű adatok kezelésénél tudjuk könnyebben áttekinteni sokaságot. Célja, hogy a sokaság összetételéről kapjunk áttekintést. Leggyakrabban osztályközös gyakoriság formájában használjuk.
Az osztályközös gyakoriság alapvetése a következő: Vegyünk egy Y ismérv valamely N számú egységéhez tartozó Y1,Y2,…Yn változatait (ezek lehetnek számszerűek és nem számszerűek is). Legyen az Y ismérv különbség- vagy arányskálán mért számérték Az Y neve változó, az Yi-ket pedig (ismérv)értékeknek nevezzük. Rendezzük sorba monoton nem csökkenő módon. Ezt nevezzük rangsornak. Nagy N esetén osztópontok kijelölésével a rangsort feldaraboljuk, ezek a részek az osztályközök. Osztályközökkel szembeni fontos követelmény, hogy azok nem fedik át egymást és az osztályközök összessége lefedi a teljes sokaságot.
3.3. táblázat - Osztályközös gyakoriság alaptáblázata
|
Az Y szerint képzett osztály |
Osztályközép | Abszolút fi |
Relatív gi | |
|---|---|---|---|---|
|
alsó |
felső | xi |
gyakoriság | |
|
határa | ||||
|
Y10 Y20 : Yi0 : Yk0 |
Y11 Y21 : Yi1 : Yk1 |
x1 x2 : xi : xk |
f1 f2 : fi : fk |
g1 g2 : gi : gk |
Összesen |
N |
1 (100%) | ||
Az osztályközös gyakoriság esetében használt fogalmak a következőek:
-
Az abszolút gyakoriság (jele: fi) megadja, hogy az adott osztályba hány darab egység tartozik sokaságból.
-
A relatív gyakoriság (jele: gi) megadja, hogy az adott osztályba tartozó elemek milyen súllyal szerepelnek a sokaságban. Számítása: gi=fi / N;
-
Az osztályközép értéke kifejezi az adott osztályköz középértékét. Számítása: xi=1/2 × (yi0 + yi1);
-
Az osztályköz hosszúság értéke az adott osztályköz két határértékének távolsága. Számítása: hii=yi1-yi0;
Első kérdés, amit el kell dönteni, hogy hány osztályközt alkossunk? A legjobb megoldás, ha az adatok ismeretében magunk határozzunk meg a szükséges osztályközök számát, de ez általában nem lehetséges. Ezért a
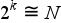 (amiből
(amiből
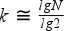 )
)
képlettel határozzuk meg a közelítő osztályköz-számot, amit szükség esetén kézzel korrigálunk.
Ha egyenletes osztályközöket akarunk képezni, akkor az osztályköz hossza:
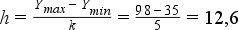
Ha egyenetlen az adatok megoszlása, akkor egyenlőtlen közöket alkalmazunk:
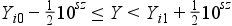
ahol sz – az ismérvérték utolsó fontos számjegyének helyértéke.
Y legyen a veszprémi légszennyezettség-mérő állomás órás NOx töménység-mérési adatai a tegnapi napra. (N = 24; Y1 jelentse az 1. óra átlagát, Y2 jelentse a 2. óra átlagát, stb.)
3.4. táblázat - Veszprémi légszennyezettség-mérő állomás órás NOx töménység-mérési adatai
|
Időpont |
Ismérv |
Érték |
Rangsort készítünk → |
Rangsor |
|
0-1 |
Y1 |
40 |
35 | |
|
1-2 |
Y2 |
45 |
36 | |
|
2-3 |
Y3 |
43 |
36 | |
|
3-4 |
Y4 |
36 |
38 | |
|
4-5 |
Y5 |
39 |
39 | |
|
5-6 |
Y6 |
46 |
39 | |
|
6-7 |
Y7 |
51 |
40 | |
|
7-8 |
Y8 |
57 |
43 | |
|
8-9 |
Y9 |
93 |
43 | |
|
9-10 |
Y10 |
98 |
45 | |
|
10-11 |
Y11 |
67 |
45 | |
|
11-12 |
Y12 |
56 |
45 | |
|
12-13 |
Y13 |
45 |
46 | |
|
13-14 |
Y14 |
56 |
51 | |
|
14-15 |
Y15 |
35 |
54 | |
|
15-16 |
Y16 |
76 |
56 | |
|
16-17 |
Y17 |
89 |
56 | |
|
17-18 |
Y18 |
92 |
57 | |
|
18-19 |
Y19 |
54 |
67 | |
|
19-20 |
Y20 |
45 |
76 | |
|
20-21 |
Y21 |
43 |
89 | |
|
21-22 |
Y22 |
38 |
92 | |
|
22-23 |
Y23 |
39 |
93 | |
|
23-24 |
Y24 |
36 |
98 |
Osztályközök száma:
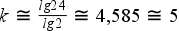
Számítása táblázatkezelő rendszerben: A kiválasztott adatsort nagyság szerint kell rendezni.
Ezt a feladatot MS Office esetén az adatok kijelölése után a következő gombbal tudjuk megtenni:
Ugyanezt a feladatot a LibreOffice-ban az adatok kijelölése után a következő gombbal tudjuk megtenni:
Egyenletes osztályköz esetén: 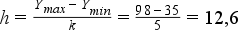
Az osztályköz táblázat a következő képen néz ki egyenletes osztályköz esetén:
3.5. táblázat - Osztályköz táblázat egyenletes osztályköz esetén
|
Yi0 |
Yi1 |
Xi |
fi |
gi |
|
35 |
47 |
41 |
13 |
~0,54 |
|
48 |
60 |
54 |
5 |
~0,21 |
|
61 |
73 |
67 |
1 |
~0,04 |
|
74 |
86 |
80 |
1 |
~0,04 |
|
87 |
99 |
93 |
4 |
~0,17 |
|
24 |
1 |
A kumulálás célja, hogy meghatározzuk hány darab adatunk (mintánk) értéke
-
kisebb vagy egyenlő (felfelé kumulált gyakoriság) illetve
-
nagyobb vagy egyenlő (lefelé kumulált gyakoriság)
mint a vizsgált osztályköz. A kumulált gyakoriság jele: fi'; A kumulált gyakoriságot lehet abszolút gyakoriságból és relatív gyakoriságból is számolni.
A kumulált gyakoriság igen gyakran használt mérőszám, ha arra vagyunk kíváncsiak, hogy a mérések közül hány darab lépte át az adott vizsgálathoz tartozó környezetvédelmi határértéket (vagy éppen maradt alatta).
A kumulálás menete a következő:
Felfelé kumulálás esetén: 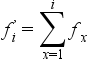 azaz ahhoz, hogy az abszolút felfelé kumulált gyakoriság értékét megkapjuk minden sorban összeadjuk az adott sor és a megelőző sorok abszolút gyakorisági (fi) értékeit.
azaz ahhoz, hogy az abszolút felfelé kumulált gyakoriság értékét megkapjuk minden sorban összeadjuk az adott sor és a megelőző sorok abszolút gyakorisági (fi) értékeit.
Lefelé kumulálás esetén: 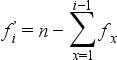 azaz ahhoz, hogy az abszolút lefelé kumulált gyakoriság értékét megkapjuk minden sorban összeadjuk az adott sor és a megelőző sorok abszolút gyakorisági (fi) értékeit, majd a kapott értéket kivonjuk a mintaszámból (n).
azaz ahhoz, hogy az abszolút lefelé kumulált gyakoriság értékét megkapjuk minden sorban összeadjuk az adott sor és a megelőző sorok abszolút gyakorisági (fi) értékeit, majd a kapott értéket kivonjuk a mintaszámból (n).
Példa: Kumulált gyakoriság
A veszprémi légszennyezettség-mérő állomás órás NOX töménység-mérési adatait alapként használva (lásd: Osztályközös gyakoriság számításának lépései) a következő eredményt kapunk:
3.6. táblázat - Kumulált gyakoriság
|
Yi0 |
Yi1 | Xi |
fi |
felfelé kumulált gyakoriság (f'i) |
lefelé kumulált gyakoriság (f' i) |
|---|---|---|---|---|---|
|
35 |
47 |
41 |
13 |
13 |
24 |
|
48 |
60 |
54 |
5 |
13+5=18 |
24-13=11 |
|
61 |
73 |
67 |
1 |
13+5+1=19 |
24-13-5=6 |
|
74 |
86 |
80 |
1 |
13+5+1+1=20* |
24-13-5-1=5** |
|
87 |
99 |
93 |
4 |
13+5+1+1+4=24 |
24-13-5-1-1=4 |
A felfelé kumulált gyakoriság számítása mind MS Excel mind LibreOffice táblázatkezelő rendszerben a következő:
3.7. táblázat - Felfelé kumulált gyakoriság számítása
|
A |
B |
C |
D |
E | |
|
1 |
Yi0 |
Yi1 |
Xi |
fi |
felfelé kumulált gyakoriság (f’i) |
|
2 |
35 |
47 |
41 |
13 |
=SZUM($D$2:D2) |
|
3 |
48 |
60 |
54 |
5 |
=SZUM($D$2:D3) |
|
4 |
61 |
73 |
67 |
1 |
=SZUM($D$2:D4) |
|
5 |
74 |
86 |
80 |
1 |
=SZUM($D$2:D5) |
|
6 |
87 |
99 |
93 |
4 |
=SZUM($D$2:D6) |
Megjegyzés: Elég az E2 cellába megírni a képletet, utána le lehet húzni az összes többi cellába.
A lefelé kumulált gyakoriság számítása mind MS Excel mind LibreOffice táblázatkezelő rendszerben a következő:
3.8. táblázat - Lefelé kumulált gyakoriság számítása
|
A |
B |
C |
D |
E | |
|
1 |
Yi0 |
Yi1 |
Xi |
fi |
felfelé kumulált gyakoriság (f’i) |
|
2 |
35 |
47 |
41 |
13 |
=SZUM($D$2:D6) |
|
3 |
48 |
60 |
54 |
5 |
=SZUM($D$2:$D$6)-SZUM($D$2:D2) |
|
4 |
61 |
73 |
67 |
1 |
=SZUM($D$2:$D$6)-SZUM($D$2:D3) |
|
5 |
74 |
86 |
80 |
1 |
=SZUM($D$2:$D$6)-SZUM($D$2:D4) |
|
6 |
87 |
99 |
93 |
4 |
=SZUM($D$2:$D$6)-SZUM($D$2:D5) |
Megjegyzés: Elég az E2 és az E3 cellába megírni a képletet, utána az utóbbit le lehet húzni az összes többi cellába.
Példa: Relatív kumulált gyakoriság
A veszprémi légszennyezettség-mérő állomás órás NOx töménység-mérési adatait alapként használva (lásd: Osztályközös gyakoriság számításának lépései) a következő eredményt kapunk:
3.9. táblázat - Relatív kumulált gyakoriság
|
Yi0 |
Yi1 |
Xi |
gi |
felfelé kumulált relatív gyakoriság (g’i) |
lefelé kumulált relatív gyakoriság (g’i) |
|
35 |
47 |
41 |
~0,54 |
0,54 |
1,00 |
|
48 |
60 |
54 |
~0,21 |
0,54+0,21=0,75 |
1,00-0,54=0,46 |
|
61 |
73 |
67 |
~0,04 |
0,54+0,21+0,04=0,79 |
1,00-0,54-0,21=0,25 |
|
74 |
86 |
80 |
~0,04 |
0,54+0,21+0,04+0,04=0,83 |
1,00-0,54-0,21-0,04=0,21 |
|
87 |
99 |
93 |
~0,17 |
0,54+0,21+0,04+0,04+0,17=1,00 |
1,00-0,54-0,21-0,04-0,04=0,17 |
Táblázatkezelő rendszerekben történő számítása megegyezik a kumulált gyakoriság (f’i) számításával.
Az osztályközökhöz az azokba tartozó egységek ismérvértékeinek szorzatát rendeli. A mennyiségi ismérv értékeinek egyes osztályokon (osztályközökön) belüli összegeit értékösszegnek nevezzük.
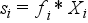
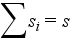
Az értékösszeg gyakorlatilag az osztályköz ismérvvel súlyozott értékét adja meg. Ez önmagában is hasznos lehet, de az értékösszegsor környezetvédelemben leggyakrabban használt formája a relatív értékösszegsor (Zi). Ebben az esetben az értékösszegeket a teljes értékösszegsorral arányosítjuk, így arányszám formájában kapjuk meg a súlyozások értékét:
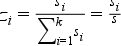
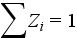
Példa:
Egy terepi mérés során 1; 3 és 5 fős mérőcsoportokat küldtek ki. A csoportok száma rendre 3; 11 és 4 darab volt. Melyik létszámú mérőcsoportban mekkora összlétszám dolgozott? Mi volt a csoportokban dolgozók egymáshoz viszonyított aránya? Melyik a legnagyobb súlyú csoport?
3.10. táblázat - Mérőcsoportok
|
Mérőcsoport létszáma (fő) Xi |
Csoportok száma (db) fi |
Mérésben résztvevők száma (fő) si |
Relatív értékösszegsor Zi |
|---|---|---|---|
|
1 |
3 |
1*3=3 |
3/56=0,054 |
|
3 |
11 |
3*11=33 |
33/56=0,589 |
|
5 |
4 |
5*4=20 |
20/56=0,357 |
|
Összesen |
18 db |
56 fő |
~1 |
A fenti feladatot mind MS Excel mind LibreOffice táblázatkezelő rendszerben a következő módon oldhatjuk meg:
3.11. táblázat - Értékösszegsor számítása.
|
A |
B |
C |
D | |
|---|---|---|---|---|
|
1 |
Mérőcsoport létszáma (fő) Xi |
Csoportok száma (db) fi |
Mérésben résztvevők száma (fő) si |
Relatív értékösszegsor Zi |
|
2 |
1 |
3 |
=A2*B2 |
=C2/$C$5 |
|
3 |
3 |
11 |
=A3*B3 |
=C3/$C$5 |
|
4 |
5 |
4 |
=A4*B4 |
=C4/$C$5 |
|
5 |
Összesen |
18 db |
=SZUM(C2:C4) |
1 |
A példa kérdésére a válasz: A legnagyobb súlyú csoport (58,9%-os részesedéssel) a három mérőszemélyből álló mérőcsoport.
A kvantiliseknek nagyon jelentős szerepük van a környezetvédelmi gyakorlatban. A kvantilisek módszere az egyenlő gyakoriságú osztályközök képzése, amely az értékek elhelyezkedéséről gyors tájékoztatást ad. Típusait az osztályközök száma alapján határozzuk meg. Ezek közül többet a gyakori használat miatt nevesítve, egyedi jelöléssel is használunk:
3.12. táblázat - Kvantilisek.
|
Osztályközök száma (k) |
Elnevezés |
Jelölés |
Lehetséges kvantilisek |
|---|---|---|---|
|
2 4 5 10 100 |
Medián Kvartilis Kvintilis Decilis Percentilis |
Me Qi Ki Di Pi |
Me Q1, Q2, Q3 K1,K2,K3,K4 D1,D2,..,D9 P1,P2,..,P99 |
A kvantilis meghatározása a következő: Az 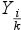 (i. k-ad rendű kvantilis szám az a szám, amelynél az összes előforduló ismérvérték
(i. k-ad rendű kvantilis szám az a szám, amelynél az összes előforduló ismérvérték 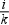 -ad része kisebb,
-ad része kisebb, 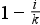 -ad része nagyobb (
-ad része nagyobb (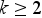 és i=1,2,…,k-1). Az
és i=1,2,…,k-1). Az 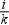 hányadost p-vel jelöljük,míg a Yp kvantilis neve p-ed rendű kvantilis. A kvantilis értékek nem feltétlenül léteztek a sorban korábban, ebben az esetben a kvantilis értékei innentől beletartoznak a sorba.
hányadost p-vel jelöljük,míg a Yp kvantilis neve p-ed rendű kvantilis. A kvantilis értékek nem feltétlenül léteztek a sorban korábban, ebben az esetben a kvantilis értékei innentől beletartoznak a sorba.
A számítás menete a következő:
1) Első lépésben meg kell határoznunk a kvantilis osztópontját (sorszámát).
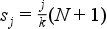
Az osztópontok száma gyakorlatilag az osztályközök számánál eggyel kisebb, azaz a medián esetén 1, kvartilis esetén 3. Ennek oka, hogy ezek a pontok határozzák meg az osztályközök töréspontjait. Fontos kiemelni, hogy ezek nem valóságos sorszámok (ezért is hívjuk őket osztópontoknak), hanem csak segédértékek. Így nem okoz gondot, hogy az esetek nagy részében ezek értéke nem egész szám.
Példa: Az „Osztályközös gyakoriság számításának lépései” fejezetnél megismert példában szereplő 24 minta esetén a kvartilis osztópontok számítása a következő:
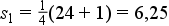
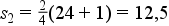
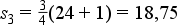
2) Ha meghatároztuk az osztópontok értékeit, akkor ki kell számolni, hogy ezek az osztópontok milyen konkrét értékekhez tartoznak, azaz mekkorák a kvantilis értékei:
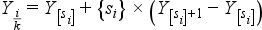
Ezek az értékek az esetek többségében nem voltak meg az eredeti értéksorban, de kiszámításuk után már részei lesznek (azaz megnövelik a sor darabszámát).
Példa:
Az „Osztályközös gyakoriság számításának lépései” fejezetnél megismert példában szereplő adatokból az előbb kiszámolt három kvartilis osztópont adatait felhasználva az osztópontok értékei a következők:
Az eredeti adattábla a következő:
3.13. táblázat - Kvantilisek meghatározásához kiindulási adattábla.
|
i |
Yi |
i |
Yi |
i |
Yi |
|---|---|---|---|---|---|
|
1 |
35 |
9 |
43 |
17 |
56 |
|
2 |
36 |
10 |
45 |
18 |
57 |
|
3 |
36 |
11 |
45 |
19 |
67 |
|
4 |
38 |
12 |
45 |
20 |
76 |
|
5 |
39 |
13 |
46 |
21 |
89 |
|
6 |
39 |
14 |
51 |
22 |
92 |
|
7 |
40 |
15 |
54 |
23 |
93 |
|
8 |
43 |
16 |
56 |
24 |
98 |
Az osztópontok a következőek:
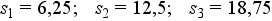
Ebből a kvantilisek:
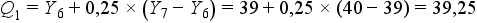
Jelentése: Mivel kvantilisről, azaz négy felé osztásról van szó, így a három kvantilis rendre  -e,
-e, 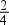 -e és
-e és 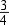 -e a teljes sornak. Így a Q1 esetében a minták 25%-a kisebb koncentrációjú, mint 39,25. (Azaz 75%-nak nagyobb a koncentrációja ennél.)
-e a teljes sornak. Így a Q1 esetében a minták 25%-a kisebb koncentrációjú, mint 39,25. (Azaz 75%-nak nagyobb a koncentrációja ennél.)
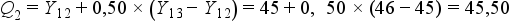
Jelentése: A minták 50%-a kisebb koncentrációjú, mint 45,50. (Azaz 50%-nak nagyobb a koncentrációja ennél.)
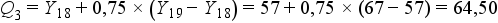
Jelentése: A minták 75%-a kisebb koncentrációjú, mint 64,50. (Azaz 25%-nak nagyobb a koncentrációja ennél.)
A környezetvédelmi adatok elemzése során sokszor kerülünk olyan probléma elé, hogy meg kell határozni egy adatsor középértékét. Ez számtalan esetben nem a matematikai átlagértéket jelenti, hanem valamilyen szempont szerinti középpontot. A leggyakrabban használt középértékek a következőek:
Helyzeti középértékek:
-
Medián (Me)
-
Módusz (Mo)
Átlagok (súlyozott és súlyozatlan, a súlyok gyakran a relatív gyakoriságok):
-
Számtani átlag (
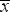 vagy
vagy 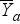 )
) -
Mértani (geometriai) átlag (
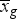 vagy
vagy 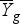 )
) -
Harmonikus átlag (
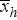 vagy
vagy 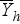 )
) -
Négyzetes átlag (
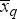 vagy
vagy 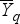 ;)
;)
Az az ismérvérték, amelynél az összes ismérvérték fele kisebb, fele pedig nagyobb. Ez gyakorlatilag a klasszikus középérték, azaz amikor a számok súlypontját keressük.
Több féle módon is számíthatjuk. Lehetőség van rangsor, kumulált gyakoriság és osztályközös gyakoriság alapján történő meghatározására.
Ha a számítás a rangsor alapján történik, különböző módon, attól függően, hogy a rangsorban lévő adatok darabszáma páratlan vagy páros:
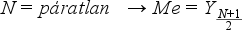
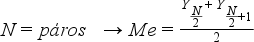
Példa:
Az „Osztályközös gyakoriság számításának lépései” fejezetnél megismert példában szereplő adatokból (24 darab adat) számítva:
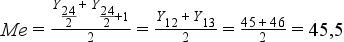 ;
;
Azaz az adatok pont fele kisebb (illetve nagyobb), mint 45,5.
Ha a számítás a kumulált gyakoriság ismerete esetén történik, akkor a következő képletet használjuk:
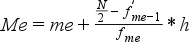
Ahol: me: mediánt magába foglaló osztályköz alsó határa
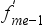 : mediánt megelőző osztályköz kumulált gyakorisága
: mediánt megelőző osztályköz kumulált gyakorisága
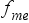 : medián osztályközének kumulált gyakorisága
: medián osztályközének kumulált gyakorisága
h: medián osztályközének hossza
Példa:
A „Kumulálás (halmozott összeadás)” fejezetnél megismert példában szereplő adatokból számítva:
3.14. táblázat - Medián számítás alapadatai felfelé kumulált gyakorisággal
|
Yi0 |
Yi1 |
Xi |
fi |
felfelé kumulált gyakoriság (f’i) |
|---|---|---|---|---|
|
35 |
47 |
41 |
13 |
13 |
|
48 |
60 |
54 |
5 |
13+5=18 |
|
61 |
73 |
67 |
1 |
13+5+1=19 |
|
74 |
86 |
80 |
1 |
13+5+1+1=20 |
|
87 |
99 |
93 |
4 |
13+5+1+1+4=24 |
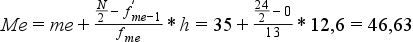
Ha a számítás a relatív gyakoriság ismerete esetén:
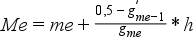 ;
;
Ahol: me: mediánt magába foglaló osztályköz alsó határa
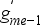 : mediánt megelőző osztályköz kumulált relatív gyakorisága
: mediánt megelőző osztályköz kumulált relatív gyakorisága
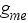 : medián osztályközének kumulált relatív gyakorisága
: medián osztályközének kumulált relatív gyakorisága
h: medián osztályközének hossza
Példa:
A „Kumulálás (halmozott összeadás)” fejezetnél megismert példában szereplő adatokból számítva:
3.15. táblázat - Medián számítás alapadatai relatív kumulált gyakorisággal
|
Yi0 |
Yi1 |
Xi |
gi |
felfelé kumulált relatív gyakoriság (g’i) |
lefelé kumulált relatív gyakoriság (g’i) |
|---|---|---|---|---|---|
|
35 |
47 |
41 |
~0,54 |
0,54 |
1,00 |
|
48 |
60 |
54 |
~0,21 |
0,54+0,21=0,75 |
1,00-0,54=0,46 |
|
61 |
73 |
67 |
~0,04 |
0,54+0,21+0,04=0,79 |
1,00-0,54-0,21=0,25 |
|
74 |
86 |
80 |
~0,04 |
0,54+0,21+0,04+0,04=0,83 |
1,00-0,54-0,21-0,04=0,21 |
|
87 |
99 |
93 |
~0,17 |
0,54+0,21+0,04+0,04+0,17=1,00 |
1,00-0,54-0,21-0,04-0,04=0,17 |
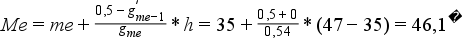
A három medián érték jelenleg a következő értéket veszi fel:
rangsorból: 45,5 < kumulált relatív gyakoriságból: 46,1 < kumulált gyakoriságból: 46,63
Ez a sorrend csak most alakult így, de nem feltétlenül így fog alakulni a sorrend, ha más kiindulási adatokkal dolgozunk!
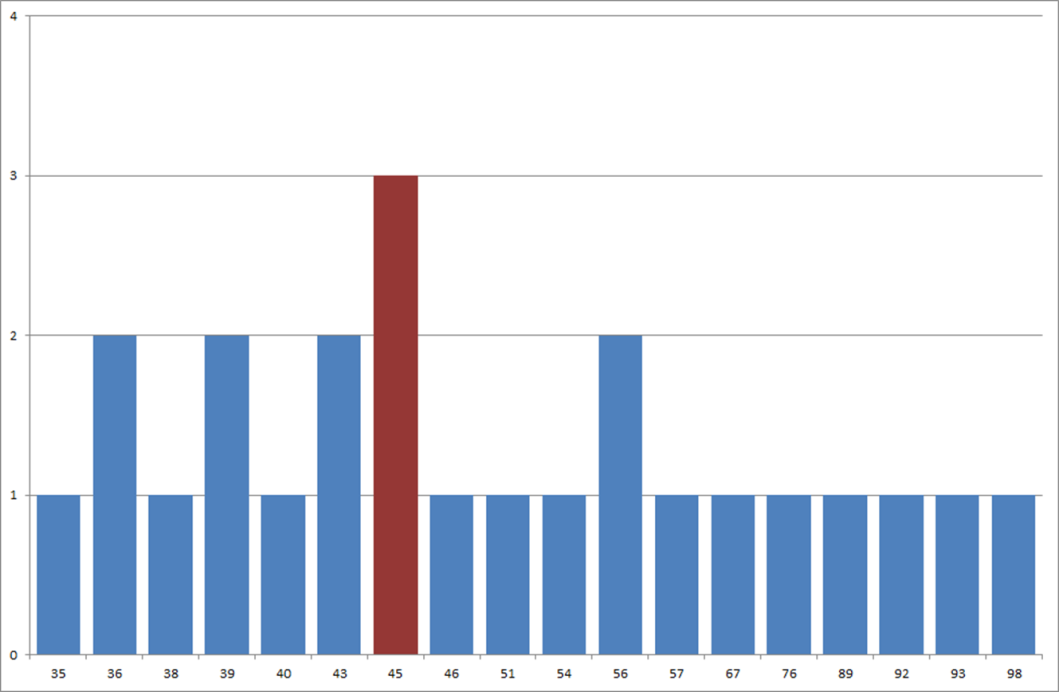
Módusznak a legtipikusabb, leggyakrabban előforduló ismérvet nevezzük. Két típus fordul elő: diszkrét esetben (amikor az adatok önálló, egymástól független értékeket vesznek fel), a leggyakoribb ismérvértéket, míg folytonos esetben (amikor az adatokat egy görbe írja le), akkor a görbe legnagyobb pontjához tartozó érték a módusz. Ez utóbbi esetben a legtöbbször új ismérvérték jön létre, ami részévé válik a sornak.
Példa:
3.16. táblázat - Módusz meghatározásának lépései
|
Rangsor |
megszámoljuk az előfordulást → |
Ismérvérték |
Előfordulás |
sorba rendezzük → |
Ismérvérték |
Előfordulás |
|
35 |
35 |
1 |
45 |
3 | ||
|
36 |
36 |
2 |
36 |
2 | ||
|
36 |
38 |
1 |
39 |
2 | ||
|
38 |
39 |
2 |
43 |
2 | ||
|
39 |
40 |
1 |
56 |
2 | ||
|
39 |
43 |
2 |
35 |
1 | ||
|
40 |
45 |
3 |
38 |
1 | ||
|
43 |
46 |
1 |
40 |
1 | ||
|
43 |
51 |
1 |
46 |
1 | ||
|
45 |
54 |
1 |
51 |
1 | ||
|
45 |
56 |
2 |
54 |
1 | ||
|
45 |
57 |
1 |
57 |
1 | ||
|
46 |
67 |
1 |
67 |
1 | ||
|
51 |
76 |
1 |
76 |
1 | ||
|
54 |
89 |
1 |
89 |
1 | ||
|
56 |
92 |
1 |
92 |
1 | ||
|
56 |
93 |
1 |
93 |
1 | ||
|
57 |
98 |
1 |
98 |
1 | ||
|
67 | ||||||
|
76 | ||||||
|
89 | ||||||
|
92 | ||||||
|
93 | ||||||
|
98 |
A számítás eredményét ábrázolva (2.4. ábra) vizuálisan is elkülöníthető a módusz. Ha nem akarjuk ábrázolni, akkor a számolás eredményének sorba rendezésével kapjuk meg az eredményt. A módusz kézi számítása nagyon időigényes folyamat, így célszerűbb táblázatkezelő rendszerre bízni annak kiszámítását.
Módusz számítása táblázatkezelő rendszerben két úton lehetséges. Ha megelégszünk a legtöbbször előforduló értékek közül a legkisebbel (azaz ha például a 39 és a 45 is háromszor fordul elő, akkor csak a 39-et fogjuk megkapni), akkor:
-
MS Excel esetében a =MÓDUSZ.EGY(tartomány) utasítással tudjuk elvégezni a számítást. (A tartomány helyébe mindig az adatokat tartalmazó mezőket kell megadni. Például: „=MÓDUSZ.EGY(A2:A25)”)
-
LibreOffice esetében a =MÓDUSZ(tartomány) utasítással tudunk eljárni.
Ez a módszer alkalmazása bár kényelmes és gyors, sokszor vezethet tévútra illetve hamis elemzéshez, ami a kézi módszernél sokkal nehezebben fordulhat csak elő. Például vegyük egy város éves óránkénti NOx töménység értékének az adatsorát (24*365=8760 adat). A táblázatkezelő által kiírt módusz érték 10 mg/m3. Ha kézzel végezzük el a számítást, akkor kiderül, hogy valóban a tízes érték fordul elő leggyakrabban az adatsorban (107-szer), de a 45-ös (103-szor) és a 44-es (98-szor) érték szorosan követi a gyakorisági sorban (a következő 19-es érték már csak 37-szer fordult elő). Ha valaki csak a táblázatkezelő értéke alapján dönt, akkor – ahogy sajnos számtalanszor előfordult már – megnyugodva közölheti: a városban leggyakrabban nagyon tiszta a levegő. Ha viszont veszi a fáradságot és elvégzi a teljes elemzést, akkor viszont gyorsan kiderül, hogy a szennyezett értékek száma jóval magasabb, mint a tízes értéké csak – például a műszer mérési jellegzetessége miatt – megoszlik két mérési érték között. Természetesen van kényelmes feloldása a gyors és esetleg félrevezető és a fáradságos, de értékesebb számítás kérdésének. Ez pedig a makro. A táblázatkezelők makro nyelvével gyorsan és hatékonyan elvégezhetjük a számítást. (A makro nyelv ismertetése nem célja ezen anyagnak, de számos kiváló forrásanyag segítheti az elsajátítását.)
A feladat megoldása makro nyelv használatával:
3.17. táblázat - Módusz meghatározása makróval.
|
A |
B |
C |
D | |
|---|---|---|---|---|
|
1 |
Ismérvek |
Értékek |
Előfordulás (db) | |
|
2 |
35 |
35* |
1* | |
|
3 |
36 |
36* |
2* | |
|
4 |
36 |
38* |
1* | |
|
5 |
38 |
39* |
2* | |
|
6 |
39 |
40* |
1* | |
|
7 |
39 |
43* |
2* | |
|
8 |
40 |
45* |
3* | |
|
9 |
43 |
46* |
1* | |
|
10 |
43 |
51* |
1* | |
|
11 |
45 |
54* |
1* | |
|
12 |
45 |
56* |
2* | |
|
13 |
45 |
57* |
1* | |
|
14 |
46 |
67* |
1* | |
|
15 |
51 |
76* |
1* | |
|
16 |
54 |
89* |
1* | |
|
17 |
56 |
92* |
1* | |
|
18 |
56 |
93* |
1* | |
|
19 |
57 |
98* |
1* | |
|
20 |
67 | |||
|
21 |
76 | |||
|
22 |
89 | |||
|
23 |
92 | |||
|
24 |
93 | |||
|
25 |
98 |
* A csillaggal jelzett számokat a makro írta be.
Megjegyzés: A makrót korlátlan számú ismérvre le lehet futtatni.
'
'Módusz
'
'(C)2011 Dr. Domokos Endre
'
Sub Módusz()
Dim t, r, s As Integer
Dim Van As Boolean
t = 2
r = 2
Do Until Cells(t, 1) = ""
Van = False
For s = 2 To r
If Cells(t, 1) = Cells(s, 3) Then
Cells(s, 4) = Cells(s, 4) + 1
Van = True
Exit For
End If
Next s
If Van = False Then
Cells(r, 3) = Cells(t, 1)
Cells(r, 4) = 1
r = r + 1
End If
t = t + 1
Loop
End Sub
A statisztikai mutatók feladata, hogy számszerűen, pontosan megmutassa egy adatsor jellemző értékeit. Míg a grafikonokon alapuló elemzéseket jellemzően az adatsorok gyors áttekintésére, emberi felhasználók számára történő látványos megjelenítésre használjuk a környezetvédelem területén, számos esetben szükségünk lehet továbbszámításokhoz használható, számszaki adatokra. Az erre szolgáló számos módszer közül terjedelmeket és a momentumokat ismertetjük részletesen.
A terjedelem mutató meghatározza, hogy az adott adatsor mekkora tartományt ölel fel, azaz mekkora a legkisebb és legnagyobb értéke.
A terjedelem meghatározásával gyorsan megállapítható például egy mérés-sorozatról, hogy annak valamelyik eleme átlépte-e a határértéket, vagy sem. A terjedelemnek két fő típusát különböztetjük meg:
-
amikor a teljes adatsorra vonatkoztatunk, akkor a „rendes” terjedelmet nézzük (jellemzően nem teszünk megkülönböztető jelzőt a megnevezés elé),
-
amikor viszont csak egy kisebb részét vizsgáljuk az egésznek (jellemzően egy vagy több kvantilist), akkor interkvantilis vagy nyesett terjedelemről beszélünk.
Példa: Az „Osztályközös gyakoriság számításának lépései” fejezetnél megismert példában szereplő 24 minta esetén, mind MS Office-ban mind LiberOffice-ban azonosan tudjuk megoldani:
3.18. táblázat - Terjedelem meghatározása.
|
A |
B |
C | |
|---|---|---|---|
|
1 |
Érték |
Terjedelem | |
|
2 |
40 |
Legkisebb |
=MIN(A2:A25) |
|
3 |
45 |
Legnagyobb |
=MAX(A2:A25) |
|
4 |
43 | ||
|
5 |
36 | ||
|
6 |
39 | ||
|
7 |
46 | ||
|
8 |
51 | ||
|
9 |
57 | ||
|
10 |
93 | ||
|
11 |
98 | ||
|
12 |
67 | ||
|
13 |
56 | ||
|
14 |
45 | ||
|
15 |
56 | ||
|
16 |
35 | ||
|
17 |
76 | ||
|
18 |
89 | ||
|
19 |
92 | ||
|
20 |
54 | ||
|
21 |
45 | ||
|
22 |
43 | ||
|
23 |
38 | ||
|
24 |
39 | ||
|
25 |
36 |
A meghatározás eredményeképpen megtudjuk, hogy a terjedelem 35 és 98 között van.
Az interkvantilis terjedelem meghatározása során egyszerűen vesszük a kiválasztott kvantilisek két szélső darabját és azok értéke lesz a terjedelem.
A leggyakrabban használt két interkvantilis terjedelem a decilisből (a középső 80%-ot szokták így meghatározni), illetve a kvartilisből képzett (így pedig a középső 50%-ot lehet meghatározni). A kvartilisből képzett értéket nagyon gyakran Box-and-whiskers módszernek is hívják.
Példa: Ábrázoljuk az „Osztályközös gyakoriság számításának lépései” fejezetnél megismert példában szereplő 24 minta esetén a Box-and-whiskers értéket a mediánhoz képest.
Vegyük a „Kvantilisek” fejezetben meghatározott kvartilis értékek kvantilisét:
Q1 = 39,25
Q2 = 45,50
Q3 = 64,50
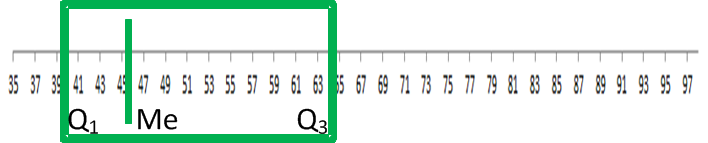
Ezután vegyük az első és a harmadik kvartilis kvantilis értéket, majd ábrázoljuk azt egy számegyenesen:
A példa jól megmutatja, hogy ha:
-
csak a teljes terjedelemre elemzünk, akkor úgy vélhetnénk, hogy nagyon szélsőséges értékek között mozog (35-98)
-
ha már a medián értékét is figyelembe vesszük (Me=45,5), akkor sokkal jobb rálátásunk lesz az adatsorra, mivel kiderül, hogy az adatok a tartomány alsóbb régiójában összpontosulnak,
-
végül – anélkül, hogy túlzottan bele kellene mélyedni az adatokba – a box-and-whiskers értékkel egészen pontosan be tudjuk határolni, hogy a jellemző mérési értékek a 39 és 65 közötti tartományban találhatóak.
A statisztikai momentumok közül az átlag és a szóródás információt nyújtanak az adatsor tekintetében a hely és a változékonyság (terjedés, megoszlás) kérdésében és ez által, megközelítő tájékoztatást nyújtanak azok eloszlásáról (mint azt például egy fényképről készült hisztogram esetében). Az átlag és a szóródás az első két statisztikai momentum, míg a harmadik és a negyedik momentumok tájékoztatást nyújtanak az eloszlás alakjáról és változékonyságáról.
Ezek az információk elsődleges célja a gyors, és hatékony adat-áttekinthetőség elérése. Ezek közül a környezetvédelemben a szóródás a leggyakrabban használt művelet.
A szóródás az átlagtól történő eltérést mutatja meg. Mérőszáma a szórás. A szórás értéke tájékoztatást ad arról, hogy mennyire egységes az adatállomány. Kifejezetten fontos érték, ha egy mérőműszer pontosságáról, egy mérés megbízhatóságáról kívánunk tudást szerezni.
Számítása súlyozott és súlyozatlan úton lehetséges. Az utóbbi módszer használata gyakoribb a mérési módszer ellenőrzésekor. Az előbbit alkalmazzuk például hatástanulmányok esetében, amikor a környezet több elemének változásának átlagos eltérésére vagyunk kíváncsiak, de a környezeti elemeket nem egyenlő súllyal kívánjuk figyelembe venni (például a vizet érintő változásokat kiemelten kívánjuk kezelni).
A számítás során gyakorlatilag az egyedi értékeket hasonlítjuk össze az átlaggal, majd negatív értékek elkerülése érdekében négyzetre emeljük és a végén az átlagból gyököt vonunk.
Súlyozatlan esetben a számítás:
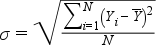
Súlyozott esetben a számítás:
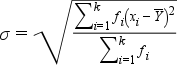
Példa:
Egy 15 km hosszú védett folyó-területen, 1 km-ként mérték fel a fajgazdagságot (hány féle fajt találtak az adott területen), illetve meghatározták a folyó vízminőségi kategóriáját. Kérdés milyen szórást mutat a folyó vízminőségi kategóriája, illetve milyen súlyozott szórást mutat ez az érték, ha figyelembe vesszük a fajgazdagságot is.
Súlyozatlan esetben, mind MS Office-ban mind LiberOffice-ban megbízható függvényt tudunk használni.
3.19. táblázat - Szórás meghatározása.
|
A | |
|---|---|
|
1 |
Kategória |
|
2 |
5 |
|
3 |
5 |
|
4 |
4 |
|
5 |
3 |
|
6 |
4 |
|
7 |
5 |
|
8 |
5 |
|
9 |
4 |
|
10 |
5 |
|
11 |
5 |
|
12 |
4 |
|
13 |
3 |
|
14 |
2 |
|
15 |
4 |
|
16 |
5 |
|
17 |
0,909* |
* MS Office esetében: =SZÓR.S(A2:A16)
* LiberOffice esetében: =SZÓRÁSP(A2:A16)
Súlyozott esetben sem a MS Office-ban sem a LiberOffice-ban nem találunk függvényt a megoldásra, így a példában szereplő 15 minta esetén, a következő képletrendszerrel tudjuk elvégezni a számítást (mindkét esetben azonos képletekkel).
3.20. táblázat - Súlyozott szórás meghatározása.
|
A |
B |
C |
D | |
|---|---|---|---|---|
|
1 |
Kategória |
Fajgazdagság |
Segédoszlop | |
|
2 |
5 |
104 |
=F2*HATVÁNY((A2-$D$3);2) |
Átlag: |
|
3 |
5 |
97 |
=F2*HATVÁNY((A3-$D$3);2) |
=ÁTLAG(A2:A16) |
|
4 |
4 |
117 |
=F2*HATVÁNY((A4-$D$3);2) |
|
|
5 |
3 |
110 |
=F2*HATVÁNY((A5-$D$3);2) |
=SZUM(B2:B16) |
|
6 |
4 |
76 |
=F2*HATVÁNY((A6-$D$3);2) |
Segédátlag |
|
7 |
5 |
140 |
=F2*HATVÁNY((A7-$D$3);2) |
=ÁTLAG(C2:C16) |
|
8 |
5 |
131 |
=F2*HATVÁNY((A8-$D$3);2) |
Szórás |
|
9 |
4 |
132 |
=F2*HATVÁNY((A9-$D$3);2) |
=GYÖK(D7/D5) |
|
10 |
5 |
107 |
=F2*HATVÁNY((A10-$D$3);2) | |
|
11 |
5 |
119 |
=F2*HATVÁNY((A11-$D$3);2) | |
|
12 |
4 |
96 |
=F2*HATVÁNY((A12-$D$3);2) | |
|
13 |
3 |
103 |
=F2*HATVÁNY((A13-$D$3);2) | |
|
14 |
2 |
89 |
=F2*HATVÁNY((A14-$D$3);2) | |
|
15 |
4 |
108 |
=F2*HATVÁNY((A15-$D$3);2) | |
|
16 |
5 |
110 |
=F2*HATVÁNY((A16-$E$3);2) |
Sok esetben a szóródás önmagában nem segít a valós helyzet felmérésben, ami számos félreértelmezéshez vezethet. Amikor kijelentjük egy mérésről, hogy a szóródása 19,62 mg/m3, az számos esetben nem ad elég tájékozódási alapot. Sok ez az érték? Kevés ez az érték? Ha például a mérés 100 000 mg/m3 nagyságrendű, akkor a szóródás kiváló mérési pontosságot takar, de ha a mérés 100 mg/m3 nagyságrendű, akkor komoly fenntartásaink lehetnek a méréssel kapcsolatban.
Ezt a bizonytalanságot csökkenti a relatív szóródás kiszámítása, ami százalékos formában adja meg a szórás és az számtani átlag hányadosát.
Számítása:
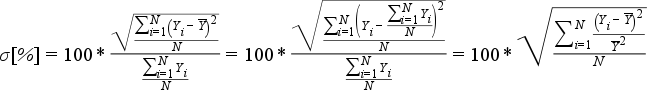
Példa:
Egy kalibrációs mérési sorozat eredményei alapján határozzuk meg a szóródást és a relatív szóródást. A megoldás mind MS Office-ban mind LiberOffice-ban beépített függvények segítségével lehetséges.
3.21. táblázat - Relatív szóródás meghatározása.
|
A |
B | ||
|---|---|---|---|
|
1 |
Mért érték (mg/l) | ||
|
2 |
104 | ||
|
3 |
103 | ||
|
4 |
98 | ||
|
5 |
101 | ||
|
6 |
102 | ||
|
7 |
99 | ||
|
8 |
100 | ||
|
9 |
100 | ||
|
10 |
98 | ||
|
11 |
102 | ||
|
12 |
103 | ||
|
13 |
104 | ||
|
14 |
102 | ||
|
15 |
103 | ||
|
16 |
101 | ||
|
17 |
Szóródás |
1,92* |
mg/l |
|
18 |
Relatív szóródás |
1,90** |
% |
* MS Office esetében: =SZÓR.S(B2:B16)
* LiberOffice esetében: =SZÓRÁSP(B2:B16)
** MS Office és LiberOffice esetében: =100*(B18/ÁTLAG(B3:B17))
A szóródás vizsgálatának egy másik elve, amelyet Corrado Gini alkotott meg, azt vizsgálja, hogy az ismérvek mennyire különböznek egymástól. Ezt a vizsgálatot általános vagy abszolút különbségnek hívjuk. Az elemzés kifejezetten hasznos, ha a szélsőségekre szeretnénk választ kapni. Ennél a vizsgálati módszernél már néhány, az átlagtól kiugróan eltérő ismérv is jelentősen megemeli a különbség értékét.
Lehetséges súlyozott és súlyozatlan módon is számolni. Képlet a következő:
Súlyozatlan:
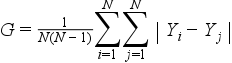
Súlyozott:
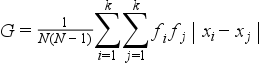
Példa:
A „Szóródás (δ)” fejezetben megismert példán számítsuk ki az átlagos különbség súlyozatlan és súlyozott értékét.
A feladatot kényelmesen MS Office-ban és LibreOffice-ban is csak makro nyelven tudjuk megoldani. A makró forráskódja a következő:
3.22. táblázat - Különbség számításához alapadatok
|
A |
B | |
|---|---|---|
|
1 |
Kategória |
Fajgazdagság |
|
2 |
5 |
104 |
|
3 |
5 |
97 |
|
4 |
4 |
117 |
|
5 |
3 |
110 |
|
6 |
4 |
76 |
|
7 |
5 |
140 |
|
8 |
5 |
131 |
|
9 |
4 |
132 |
|
10 |
5 |
107 |
|
11 |
5 |
119 |
|
12 |
4 |
96 |
|
13 |
3 |
103 |
|
14 |
2 |
89 |
|
15 |
4 |
108 |
|
16 |
5 |
110 |
|
17 |
Átlagos |
különbség |
|
18 |
Súlyozatlan |
1,00952381* |
|
19 |
Súlyozott |
11554,01905* |
* A csillaggal jelzett számokat a makro írta be.
'
'Átlagos különbség számítása
'
'(C)2011 Dr. Domokos Endre
'
Sub Súlyozatlan()
Dim r, t, N As Integer
Dim Különbség, G As Double
N = 15
Különbség = 0
For t = 2 To N + 1
For r = 2 To N + 1
Különbség = Különbség + Abs(Cells(t, 1) - Cells(r, 1))
Next r
Next t
G = (1 / (N * (N - 1))) * Különbség
Cells(N + 3, 2) = G
End Sub
Sub Súlyozott()
Dim r, t, N As Integer
Dim Különbség, G As Double
N = 15
Különbség = 0
For t = 2 To N + 1
For r = 2 To N + 1
Különbség = Különbség + (Cells(t, 2) * Cells(r, 2) * Abs(Cells(t, 1) - Cells(r, 1)))
Next r
Next t
G = (1 / (N * (N - 1))) * Különbség
Cells(N + 4, 2) = G
End Sub
A szóródások egy különleges fajtája a momentum képzés, amelynek során a szóródást egy tetszőlegesen kiválasztott (akár az ismérvek között nem szereplő) értékhez viszonyítjuk. Kiválóan lehet használni e módszert műszerek teljes pontosságának meghatározására, amikor egy ismert (beállító) érték mérése során mért értékeket viszonyítunk a beállító értékhez.
Gyakorlatban a momentum képzés az átlagok és a szórások általános felírása. Általános megfogalmazása a következő: Y ismérv vagy gyakorisági eloszlás A körüli r-ed rendű momentumai.
Számítása súlyozatlan esetben:
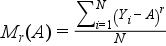
Súlyozott esetben:
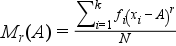
Néhány nevezetes momentum:
Számtani átlag (r=1, A=0):
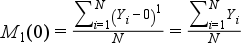
Négyzetes átlag négyzete (r=2, A=0):
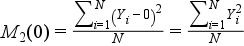
Variancia (r=2, 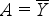 ):
):
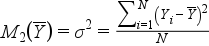
Megbízhatóság (r=2, A =beállító érték)
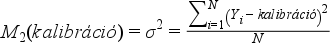
Példa:
A „Relatív szóródás” fejezetben megismert példa során a mérést 100 mg/l-es sűrűségű mintával végeztük. Számítsuk ki a megbízhatóságát a berendezésnek.
3.23. táblázat - Momentum számítás (berendezés megbízhatósága)
|
A |
B |
C |
D | |
|---|---|---|---|---|
|
1 |
Mért érték (mg/l) |
Segédoszlop |
Beállító sűrűség | |
|
2 |
104 |
=HATVÁNY(B2-$D$2;2) |
100 | |
|
3 |
103 |
=HATVÁNY(B3-$D$2;2) |
mg/l | |
|
4 |
98 |
=HATVÁNY(B4-$D$2;2) | ||
|
5 |
101 |
=HATVÁNY(B5-$D$2;2) | ||
|
6 |
102 |
=HATVÁNY(B6-$D$2;2) | ||
|
7 |
99 |
=HATVÁNY(B7-$D$2;2) | ||
|
8 |
100 |
=HATVÁNY(B8-$D$2;2) | ||
|
9 |
100 |
=HATVÁNY(B9-$D$2;2) | ||
|
10 |
98 |
=HATVÁNY(B10-$D$2;2) | ||
|
11 |
102 |
=HATVÁNY(B11-$D$2;2) | ||
|
12 |
103 |
=HATVÁNY(B12-$D$2;2) | ||
|
13 |
104 |
=HATVÁNY(B13-$D$2;2) | ||
|
14 |
102 |
=HATVÁNY(B14-$D$2;2) | ||
|
15 |
103 |
=HATVÁNY(B15-$D$2;2) | ||
|
16 |
101 |
=HATVÁNY(B16-$D$2;2) | ||
|
17 |
Megbízhatóság |
=SZUM(C2:C16)/DARAB(B2:B16) |
mg/l |
Az eredmény 5,47 mg/l, azaz a berendezésünk által mért értékek ±6 mg/l pontosak (ez a műszerünk megbízhatósága).
Tartalom
Az Európai Unió illetve Magyarország környezetpolitikájában egyre nagyobb szerepet kap a társadalom, mivel növekszik az emberek környezettudatossága és a környezeti információk iránt az igényük. Alapvető fontosságú, hogy a lakosság tájékozódni tudjon lakóhelyének környezeti állapotáról, és így lehetősége nyílik részt venni a döntési folyamatokban. Ahhoz, hogy ez a rendszer kialakuljon, közérthető formában kell az emberek elé tárni az adott problémát.
A demokrácia fejlődésével egyre inkább előtérbe kerül az önkormányzatok felelősségében, a településeken lakók számára élhető és egészséges környezet megteremtése, és az, hogy olyan területfejlesztési programokat indítsanak, mely ezt elősegíti. A környezeti információk megléte, látványos megjelenítése jelentősen megkönnyíti a területfejlesztési döntések meghozatalát, a fejlesztések kapcsán a lakosság informálását, egy esetleges lakossági fórum, vagy szavazás szakmai megalapozását.
A törvényeknek megfelelően mára több állami szervezet, és önkormányzat biztosít hozzáférést a környezeti adatokhoz, és azok értékeléséhez. A civil társadalomra jellemző módon, az állam mellett több civil szervezet önként vállat, vagy szerződésben rögzített feladatként foglalkozik környezeti információs rendszerek építésével és lakossági tájékoztatással. Ezek mellett több állami és non-profit kutatóhely munkakörébe tartozik a környezeti adatok gyűjtése, értékelése.
Ennek ellenére be kell látnunk, hogy mind a lakossági tájékoztatás, mind pedig a nyilvánosan hozzáférhető adatbázisok működése napjainkban még gyenge lábakon áll hazánkban. Számos oldalon például csak utalásokat találhatunk bizonyos adatbázisokra, ezek lenyíló választó fülei is megjelennek, azonban ezek után vagy csak egy rövid szöveges leírást találunk, vagy éppen egy jelszóval védett oldalra jutunk. Így kimaradnak a felsorolásból olyan oldalak, mint:
-
Vízügyi honlap
-
Vízügyi és Környezetvédelmi Központi Igazgatóság
Vízgazdálkodási Információs Rendszer (VIZIR).
Vízkárelhárítási Védekezési Információs Rendszer (VIR).
Vízminőségi Kárelhárítási Információs Rendszer (VIKÁR).
Hidrometeorológiai Információs Rendszer.
Vízföldtani Információs Rendszer.
Vízügyi jelentés nyilvántartási információs rendszer.
-
Települési Szennyvíz Információs Rendszer
-
Talajvédelmi Információs Monitoring Rendszer (TIM)
Tekintettel arra, hogy minden területnek megvan a maga adatbázisa, jelen fejezetben elsősorban a környezetvédelmi jellegű, illetve az azzal összefüggésbe hozható (jelentősebb) adatbázisokat tekintjük át. Kizárólag olyan adatlapok kerülnek megemlítésre, amelyek nem csak felsorolják, hogy az adott szervezet milyen jellegű adatokat gyűjt, hanem amelyek ténylegesen online, mindenki számára elérhető, lekérhető adatokat is szolgáltat a környezettel kapcsolatosan.
A Vidékfejlesztési Minisztérium (korábban Környezetvédelmi és Vízügyi Minisztérium[1], www.kvvm.hu[2]) irányítása alá tartozó szervezeteknél a környezet terhelésével és a környezet állapotával kapcsolatban számos adat áll rendelkezésre.
Az OKIR adatbázisban szereplő adatok egy része a területi környezetvédelmi szervek saját méréseiből, másik része a környezethasználók jogszabályi előírásai alapján tett adatszolgáltatásaiból származnak.
Az adatok jelentős része ma már közvetlenül központi számítógépes adatbázisba kerül, olyan módon, hogy a méréseket végző, valamit az adatszolgáltatásokat feldolgozó Környezetvédelmi, Természetvédelmi és Vízügyi Felügyelőségek a minisztériumi szerverhez kapcsolódva közvetlenül a központi adatbázisba viszik fel az adatokat. Ez a rendszer az Országos Környezetvédelmi Információs Rendszer (OKIR).
A rendszer elsődleges feladata, hogy a környezet állapotának és használatának figyelemmel kísérését, igénybevételi és terhelési adatainak gyűjtését, feldolgozását és nyilvántartását támogassa, és az érintett felhasználókat (beleértve a nyilvánosságot is) ellássa a szükséges információkkal. Moduláris felépítésű, amely azt jelenti, hogy a különböző környezetvédelmi szakterületek adatai saját szakterületi nyilvántartásokba kerülnek, amely szakrendszerek egymással összefüggő és egymás között átjárható konglomerátumot alkotnak.
A lekérdező funkció segítségével jelenleg az alábbi környezetvédelmi területekről érhetők el adatok:
-
Mi van a környezetemben? - Térképes lekérdező, a Környezetvédelmi Alapnyilvántartó Rendszerben nyilvántartott objektumok és az azokról rendelkezésre álló környezetvédelmi adatok megjelenítése érdekében
-
Hulladékgazdálkodási adatok a Hulladékgazdálkodási Információs Rendszerből (HIR)
-
Légszennyező anyag kibocsátások a Levegő-tisztaság Védelmi Információs Rendszerből (LAIR)
-
Felszíni vízminőségi mérési eredmények - a felügyelőségi laboratóriumok vízvizsgálatai mérései alapján a '60-as évekig visszamenőleg (FEVI)
-
Jogerős környezetvédelmi hatósági határozatok adatai, amelyek a felügyelőségek által vezetett Hatósági Nyilvántartó Rendszerből (HNYR) származnak
-
Veszélyes és nem veszélyes hulladékok kezelésére feljogosító engedélyek adatai, beleértve a hulladékok begyűjtésére és szállítására vonatkozó engedélyeket.
Tekintsünk meg egy példát. Kiválasztunk egy várost „Mi van a környezetemben” menüpont alatt (ez esetben Veszprémet), majd lekérdezzük, milyen levegőt terhelő pontforrások vannak a választott városunkban (3.1. ábra és 3.2. ábra).
Az adatbázisban szereplő telephelyek megjelennek a térképen. Egérrel rámutatunk az egyik piros „léggömbre”, kinyílik a címke: Volán telephely. A részletes adatokra kattintva táblázatban megnyílnak a mért a szennyezőanyag koncentrációk éves átlagai (3.2. ábra).
Az Országos Környezetvédelmi, Természetvédelmi és Vízügyi Főfelügyelőség a vidékfejlesztési miniszter irányítása alatt működő központi hivatal, önállóan működő és gazdálkodó, közhatalmi központi költségvetési szerv, illetékessége az ország egész területére kiterjed.
Felügyeleti szerve a Vidékfejlesztési Minisztérium. Közigazgatási eljárásban az alárendeltségben működő 10 környezetvédelmi, természetvédelmi és vízügyi felügyelőség (területi szerv) felettes, valamint felügyeleti szerve.
Környezetvédelmi, természetvédelmi és vízügyi felügyelőségek:
Közép-Duna-völgyi Környezetvédelmi, Természetvédelmi és Vízügyi Felügyelőség (Budapest)
Alsó-Tisza-vidéki Környezetvédelmi, Természetvédelmi és Vízügyi Felügyelőség (Szeged)
Dél-dunántúli Környezetvédelmi, Természetvédelmi és Vízügyi Felügyelőség (Pécs)
Észak-dunántúli Környezetvédelmi, Természetvédelmi és Vízügyi Felügyelőség (Győr)
Észak-magyarországi Környezetvédelmi, Természetvédelmi és Vízügyi Felügyelőség (Miskolc)
Felső-Tisza-vidéki Környezetvédelmi, Természetvédelmi és Vízügyi Felügyelőség (Nyíregyháza)
Közép-dunántúli Környezetvédelmi, Természetvédelmi és Vízügyi Felügyelőség (Székesfehérvár)
Közép-Tisza-vidéki Környezetvédelmi, Természetvédelmi és Vízügyi Felügyelőség (Szolnok)
Nyugat-dunántúli Környezetvédelmi, Természetvédelmi és Vízügyi Felügyelőség (Szombathely)
Tiszántúli Környezetvédelmi, Természetvédelmi és Vízügyi Felügyelőség (Debrecen)
A felügyelőségek weboldalai környezeti és közérdekű adatokat egyaránt tartalmaznak az elektronikus információszabadságról szóló 2005. évi XC. törvény által meghatározott formában és tartalommal. Elérhető az éppen az aktuális jogszabályok jegyzéke, továbbá a legtöbb ügyintézéshez szükséges formanyomtatvány.
1974 és 2001 között a mérőhálózatot (korábbi nevén: Országos Immisszió-mérő Hálózat) az egészségügyi tárca szakmai irányításával az akkori megyei (fővárosi) KÖJÁL-ok, majd ezek utódai, a megyei (fővárosi) ÁNTSZ intézetek üzemeltették. A mérőhálózat üzemeltetéséért 2002. február 1. óta a környezetvédelmi tárca, 2010-től a Vidékfejlesztési Minisztérium a felelős. A tényleges kezelői feladatokat a területi szervei, a környezetvédelmi, természetvédelmi és vízügyi felügyelőségek (felügyelőségek) látják el.
Az Országos Légszennyezettségi Mérőhálózat két részből áll: az automata és a manuális mérőhálózatból. A mérőhálózat az ország területén a légszennyezettség mérésére és értékelésére hivatott, mely az automatikus mérőhálózat, a manuális mérőhálózat, mobil mérőállomások és időszakos mintavételek segítségével valósul meg. Az egyes illetékességi területeken a Környezetvédelmi Felügyelőségek üzemeltetik a manuális (szakaszos) és az automatikus (folyamatos) mérőhálózat állomásait, valamint ők végzik az időszakos légszennyezettségi méréseket is.
Jelenleg 31 település 52 mintavételi helyén mérik folyamatosan a kiemelt jelentőségű légszennyező anyagok koncentrációit és az értékeléshez szükséges meteorológiai paramétereket.
Az automata mérőhálózatban mért légszennyező anyagok (nem mérnek minden komponenst minden helyszínen, példa 3.3. ábra):
-
SO2
-
NO/NO2/NOx,
-
CO
-
O3
-
Szálló por (PM10 és PM2,5 frakciók, utóbbi csak 4 helyszínen)
-
BTEX
-
H2S
-
VOC
Az automata mérőhálózatban regisztrált meteorológiai paraméterek:
szélsebesség,
szélirány,
hőmérséklet,
páratartalom,
csapadékmennyiség.
A manuális mérőhálózat (korábbi nevén: RIV: Regionális Immisszió Vizsgáló Hálózat) közel harminc éves múltra tekint vissza. A minták elemzését a szakaszos (24 órás) mintavételt követően a Környezetvédelmi, Természetvédelmi és Vízügyi Felügyelőségek akkreditált vizsgáló laboratóriumaiban végzik. A vizsgálati eredmények a felügyelőségi alközpontokba, majd végül az Országos Légszennyezettségi Adatközpontba kerülnek. Jelenleg 131 településen működik a manuális mérőhálózat. A manuális hálózatban vizsgált komponensek:
-
SO2,
-
NO2,
-
ülepedő por (g/m2*30 nap).
A háttér-szennyezettséget mérő hálózatot – négy mérőállomással - az Országos Meteorológiai Szolgálat üzemelteti, amelyek K-pusztán, Nyírjesen, Farkasfán és Hortobágyon találhatók. További két állomás működik a környezetvédelmi felügyelőség kezelésében, ezek a Fertőújlaki (Sarród) és a Majláth-pusztai mérőállomások.
Az előzőekben említett manuális és automata mérőállomások adatai a Központi Statisztikai Hivatal adatbázisában is megjelennek, továbbá bővebb információk érhetők el a metainformációs adatbázisból mind a környezetvédelmi ipar, környezetvédelmi ráfordítás, hulladék, mind pedig víz tématerületeken.
A fenti menüsorból az alábbiak szerint választhatjuk ki az adatbázisból a számunkra értékes információt.
Online adatbázisából a meteorológiai paraméterek alakulását ismerhetjük meg (mint hőmérséklet, páratartalom, szélsebesség, szélirány, UV-B sugárzás – 3.6 ábra és 3.7 ábra). Az OMSZ üzemelteti továbbá a háttérszennyezettséget mérő mérőállomásokat, méri a troposzférikus ózon koncentrációt, felszín-légkör közötti CO2 forgalmat, üvegházgáz mérlegeket készít, stb., de ez utóbbiak adatai online nem elérhetők.
Tiszta-vízgyűjtő monitoring rendszer mérési/mintavételi pontjai a 3.8 ábrán láthatók.
A monitorállomások felszereltségének főbb összetevői a mérőműszerek, a mintaellátó szivattyúrendszer, a hidraulikai rendszer, a különböző segédberendezések és a mérésvezérlő-adatgyűjtő rendszer. Online megismerhető adatok (3.1 táblázat):
4.1. táblázat - Monitorállomások alap-műszerezettsége
|
Monitorállomások alap-műszerezettsége | |||
|---|---|---|---|
|
Vízminőségi paraméter |
Mértékegység |
Mérési tartomány |
Működési elv |
|
Vízhőmérséklet |
C° |
0-50 |
Digitális |
|
pH |
0-14 |
Potenciometria | |
|
Oldott oxigén |
mg/l |
0-20 |
Voltametria |
|
Vezetőképesség |
µS/cm |
0-2000 |
Konduktometria |
|
Zavarosság |
NTU |
0-500 |
Fényvisszaszórás |
|
Ammónium ion |
mg/l |
0-10 |
Fotometria |
|
TOC |
mg/l |
0-20 |
UV gyorsított oxidáció |
|
Felszíni olaj |
- |
- |
Felszíni vízminta TOC méréshez |
|
Klorofill-a |
µg/l |
0,1-től |
Fluorometria |
|
0-20 |
T-index |
0-100 |
Daphina / Alga |
|
További műszerezettség az MS-2 monitorállomáson | |||
|
Nehézfém analizátor (cink, kadmium, ólom, réz) |
µg/l |
0-5000 |
Polarográfia |
|
Nitrát |
µg/l |
0-10 |
Fotometria |
|
Cianid |
µg/l |
0-2 |
Polarográfia |
Az országos vízminőségi törzshálózat kialakítására 1968-1972 között került sor, ennek részeként a Drávai megfigyelések már 1968-ban megkezdődtek.
-
Vízrajzi monitoring (online elérhető)
-
Vízkémiai monitoring (pH, Fajlagos vezetőképesség (µS/cm), Oldott O2 (mg/l), O2 (%), KOIsp (mg/l), KOIcr (mg/l), NH4+ (mg/l), Összes P (mg/L), a-klorofill (mg/m3), szaprobitás index) (online elérhető)
-
Biológiai monitoring
Egyesült Királyság
-
Elérhetőség: http://www.airquality.co.uk/archive/index.php
Írország
Ausztrália
Svájc
-
Elérhetőség:http://www.umweltschweiz.ch/buwal/eng/fachgebiete/fg_luft/luftbelastung/karten/index.html
Németország
-
Elérhetőség: http://www.env-it.de/luftdaten/map.fwd?measComp=O3
Franciaország
-
Elérhetőség: http://www.airnormand.asso.fr/normand/uk/index.html
A nemzetközi kitekintésből egyértelműen kiderült, hogy a vizsgált rendszerek mindegyike elsősorban a levegőminőség szempontjából jellemzi a városi környezet élhetőségét. Közös ezekben, a rendszerekben az, hogy a leggyakoribb szennyezők (O3, CO, SO2, PM10, NO, NO2, benzol) előfordulását mérik a légkörben, általában a város fixen meghatározott pontjain. Ez a megállapítás a rendszerekkel szemben támasztott alapvető elvárások közé sorolható, csakúgy, mint a megfigyelt adatok visszakereshetőségére vonatkozó kitétel. A legtöbb alkalmazás kitér a mérési eredmények minősítésére is, azaz valamilyen formában jelzi azt, hogy mennyire szennyezett adott területen a levegő. Ez általában egy – az adott ország törvényi rendelkezéseitől függő – határérték táblázat alapján történő értékelésének eredményeképpen valósul meg. A megjelenítést és az adatok böngészését egy internetes felület segítségével valósítják meg, melyen általában egy statikus térképet is alkalmaznak. Az új alkalmazásokkal szembeni elvárás mára már az, hogy az adatokat dinamikus térképeken lehessen szemléltetni, megkönnyítve ezzel az adatok elérését.
Európai Unió
E-PRTR – The European Pollutant Release and Transfer Register – 27 EU tagállam, valamint Izland, Liechtenstein, Norvégia, Szerbia és Svájc tartozik a nyilvántartásba. Éves adatokat láthatunk 28000 ipari létesítmény kapcsán, 65 gazdasági tevékenységgel összefüggésben, 9 szektorra osztva:
-
energia
-
termelés és fémfeldolgozás
-
ásványipar
-
vegyipar
-
hulladék-és vízgazdálkodás
-
papír és faanyag előállítása és feldolgozása
-
intenzív állattartás és akvakultúra
-
állati és növényi eredetű termékek az élelmiszer-és üdítőital-ágazatban, valamint egyéb tevékenységek.
EEA – European Environment Agency – Az oldal olyan környezeti kérdésekkel foglalkozik, mint például a fenntarthatóság, a környezetbarát gazdaság, a víz, a hulladék, az élelmiszer, az irányítás és az ismeretek megosztása.
-
Hivatalos nyelven: http://www.eea.europa.eu/ ( http://www.eea.europa.eu/hu)
Eurostat – Your key to European Statistics
[1] Környezetvédelmi és Vízgazdálkodási Minisztérium (1987)
Környezetvédelmi és Területfejlesztési Minisztérium (1994)
Környezetvédelmi Minisztérium (1997)
Környezetvédelmi és Vízügyi Minisztérium (2002)
Vidékfejlesztési Minisztérium (2010)
[2] Az új kormányzati portál 2011. január 1. óta él: http://www.kormany.hu./hu/videkfejlesztesi-miniszterium
Tartalom
A Magyar Köztársaság valamennyi állami és önkormányzati szerve adatok, dokumentumok sokaságát kezeli. Ezek egy része a nyilvánosság elől törvény által védett adat, más része bárki által megismerhető. Van köztük olyan, amely természetes személyre vonatkozik, van, ami az adott szervezet működésére, és létezik olyan is, amelyet a közszféra szervei a feladatuk ellátása során más szervezetekről tartanak nyilván. Az adatok kezelését, gyűjtését, továbbítását jogi normák szabályozzák.
Magyarországon az Alkotmány (az 1949. évi XX. törvény) kimondja, hogy mindenkit megillet a személyes adatok védelméhez való jog (59. § (1) bekezdés), és mindenkinek joga van arra, hogy a közérdekű adatokat megismerje és terjessze (61. § (1) bekezdés).
Az 1989–90-es politikai átalakulás egyik sarkalatos kérdése volt a nyilvánosság ügye. A rendszerváltás politikai erői egyetértettek abban, hogy nem elég a sajtószabadság, a véleménynyilvánítás szabadságának megteremtése. Egy demokratikus társadalomban elengedhetetlen, hogy szigorú törvények óvják a polgárok magánéletét, ugyanakkor biztosítsák az állam átláthatóságát, elszámoltathatóságát. Ezek alapján az Országgyűlés megalkotta a személyes adatok védelméről és a közérdekű adatok nyilvánosságáról szóló 1992. évi LXIII. törvényt (továbbiakban Avtv.), egy normába foglalva e jogok gyakorlásának legfontosabb szabályait, garanciáit.Az Avtv. alapján a közszférában kezelt adatokat öt csoportra osztjuk. 2. § E törvény alkalmazása során:
1. személyes adat: bármely meghatározott (azonosított vagy azonosítható) természetes személlyel (a továbbiakban: érintett) kapcsolatba hozható adat, az adatból levonható, az érintettre vonatkozó következtetés. A személyes adat az adatkezelés során mindaddig megőrzi e minőségét, amíg kapcsolata az érintettel helyreállítható. A személy különösen akkor tekinthető azonosíthatónak, ha őt - közvetlenül vagy közvetve - név, azonosító jel, illetőleg egy vagy több, fizikai, fiziológiai, mentális, gazdasági, kulturális vagy szociális azonosságára jellemző tényező alapján azonosítani lehet;
2. különleges adat: a) a faji eredetre, a nemzeti és etnikai kisebbséghez tartozásra, a politikai véleményre vagy pártállásra, a vallásos vagy más világnézeti meggyőződésre, az érdek-képviseleti szervezeti tagságra, b) az egészségi állapotra, a kóros szenvedélyre, a szexuális életre vonatkozó adat, valamint a bűnügyi személyes adat;
3. bűnügyi személyes adat: a büntetőeljárás során vagy azt megelőzően a bűncselekménnyel vagy a büntetőeljárással összefüggésben, a büntetőeljárás lefolytatására, illetőleg a bűncselekmények felderítésére jogosult szerveknél, továbbá a büntetés-végrehajtás szervezeténél keletkezett, az érintettel kapcsolatba hozható, valamint a büntetett előéletre vonatkozó személyes adat;
4. közérdekű adat: az állami vagy helyi önkormányzati feladatot, valamint jogszabályban meghatározott egyéb közfeladatot ellátó szerv vagy személy kezelésében lévő, valamint a tevékenységére vonatkozó, a személyes adat fogalma alá nem eső, bármilyen módon vagy formában rögzített információ vagy ismeret, függetlenül kezelésének módjától, önálló vagy gyűjteményes jellegétől;
5. közérdekből nyilvános adat: a közérdekű adat fogalma alá nem tartozó minden olyan adat, amelynek nyilvánosságra hozatalát vagy hozzáférhetővé tételét törvény közérdekből elrendeli;
Európai Unió hatodik környezetvédelmi akcióprogramja (2002-2012) külön területként jelöli meg az állampolgárok bevonásának ösztönzését a környezetvédelmi eljárásokba, illetve megfelelő jogosítványokkal való felhatalmazásukat. A társadalmi részvétel és ezzel együtt a civil kontroll mind teljesebb érvényre juttatása alapvető követelményként jelent meg a környezetvédelmi jog XX. századi fejlődésében.
A társadalmi részvétel egyes területeit a Riói Nyilatkozat 10. elve foglalja össze: ”A környezeti ügyeket a legjobban az összes érdekelt állampolgár részvételével a megfelelő szinten lehet kezelni. Nemzeti szinten minden egyénnek biztosítani kell a megfelelő hozzáférést a környezetre vonatkozó információkhoz, melyekkel a közhivatalok és a hatóságok rendelkeznek; beleértve a veszélyes anyagokra és az állampolgárok közösségeit érintő tevékenységekre vonatkozó információt; és lehetővé kell tenni a döntéshozatali folyamatban való részvételt. Az államok segítsék el és bátorítsák a lakosság tudatosságát és részvételét azzal, hogy széles körben hozzáférhetővé teszik az információkat."
A társadalmi részvétel érvényesülésének és érvényesítésének alapdokumentuma az 1998. évi Aarhusi Egyezmény, amit az Európai Parlament és a Tanács 2006. szeptember 6-i 1367/2006/EK rendelete az Európai Unió jogrendszerének szerves részévé tett. Az Egyezmény 1. cikkelye kimondja: „A jelen és jövő generációkban élő minden egyén azon jogának védelme érdekében, hogy egészségének és jólétének megfelelő környezetben éljen, ezen Egyezményben Részes valamennyi Fél garantálja a nyilvánosság számára a jogot az információk hozzáférhetőségéhez, a döntéshozatalban való részvételhez és az igazságszolgáltatás igénybevételéhez a környezetvédelmi ügyekben."
A környezet védelmének általános szabályairól szóló 1995. évi LIII. tv. (Környezetvédelmi törvény) 12. §-a tájékozódás, tájékoztatás és nyilvánosság elveként valami hasonló alapelv kimondására törekszik, de ezt a törvényi elvet csak a törvény VIII. fejezetével együtt elemezve – nyilvánosság részvétele a környezetvédelemben – azonosíthatjuk a társadalmi részvétel elvével.
A tájékozódás a környezetre vonatkozó információk megismerését jelenti, a tájékoztatás az állami szervek és önkormányzatok adatgyűjtési és ezen alapuló tájékoztatási kötelezettségével azonosítható, míg a környezethasználót is tájékoztatási kötelezettség terheli a 12. § (9) bekezdése szerint.
Az információ a társadalmi részvétel legalapvetőbb feltétele, amely két nagy jogosítványcsoportba sorolható:
-
az aktív információhoz való jutás szabályainak csoportjába, amely szerint a társadalmat rendszeresen tájékoztatni kell a környezet állapotáról, és
-
a passzív információs jog csoportjába, amelynek értelmében a társadalom tagjai vagy csoportjai információt kérhetnek, mégpedig anélkül, hogy ennek indokait meg kellene határozniuk. Az információ iránti igény visszautasítására csak indokolt esetekben kerülhet sor – ilyen lehet például a nemzetbiztonság vagy a szolgálati titok.
Az Avtv. szerint tehát: a közfeladatot ellátó szerveknek lehetővé kell tenniük, hogy a kezelésükben lévő közérdekű adatot bárki megismerhesse, kivéve,
-
ha az adott törvény alapján az arra jogosult szerv állam vagy szolgálati titokká nyilvánította, továbbá
-
ha a közérdekű adatok nyilvánosságához való jogot – az adatfajták meghatározásával – a törvény honvédelmi, nemzetbiztonsági, bűnüldözési vagy bűnmegelőzési, központi pénzügyi vagy devizapolitikai érdekből, külügyi kapcsolatokra, nemzetközi szervezetekkel való kapcsolatokra, bírósági eljárásra tekintettel korlátozza.
Információszabadság alatt azt értjük, hogy a tág értelemben vett állam működésének átláthatónak kell lennie az egyének, csoportjaik vagy akár az egész közvélemény számára, az államnak csak szigorúan és pontosan meghatározott feltételek fennállása esetén, rendkívül szűk körben lehetnek titkai. Az információszabadság számos egyéni és társadalmi célt szolgálhat, például hozzásegítheti a magánszemélyeket ügyeik gyors és egyszerű elintézéséhez, tudományos kutatókat kutatásuk alapjául szolgáló adatok megismeréséhez, vagy akár szolgálhatja bárki érdeklődésének egyszerű kielégítését is.
Az elmúlt évtizedek információs technológiájának viharos fejlődése érthető módon hatással van az információs jogok szabályozására és gyakorlatára egyaránt. A 90-es évek második felétől hazánkban is sorra jelentek meg olyan szabályok, amelyek meghatározott információk elektronikus közzétételi kötelezettségét írták elő.
2005-ben megszületett az elektronikus információszabadságról szóló 2005. évi XC. törvény (Eitv.). Az Avtv-ben biztosított jogokkal összhangban további pontosításokat jelent a jogok és kötelezettsége rendszerében. A fő gondolatmenetet a törvény célja fogalmazza meg az alábbiak szerint:
„1. § E törvény célja annak biztosítása, hogy a közvélemény pontos és gyors tájékoztatása érdekében a közérdekű adatok e törvényben meghatározott körét elektronikus úton bárki számára személyazonosítás és adatigénylési eljárás nélkül, folyamatosan és díjmentesen közzétegyék.”
Környezetvédelmi adatbázisok révén jelen témakörben alapvető fontosságú meghatározni, hogy mit is értünk „környezeti információ” alatt. A 311/2005. (XII. 25.) Korm. rendelet a nyilvánosság környezeti információkhoz való hozzáférésének rendjéről c. rendelet részletesen definiálja a környezeti információ fogalmát (az Aarhusi Egyezmény 2. cikkének 3. bekezdésével összhangban). Környezeti információ minden olyan információ (adat), amely vonatkozik:
-
a környezetre, illetve a környezeti elemek állapotára - ideértve a biológiai sokféleséget és annak összetevőit, valamint a géntechnológiával módosított szervezeteket -, valamint az ezen elemek közötti kölcsönhatásra;
-
a környezetterhelésre, ideértve a zaj, sugárzás, hulladék, radioaktív hulladék környezetbe történ közvetlen vagy közvetett kibocsátására, ha az hatással van, vagy valószínűleg hatással lehet a környezet a) pontban meghatározott elemeire;
-
környezettel összefügg intézkedésekre, különösen az azokkal kapcsolatos ágazati politikára, jogszabályokra, tervekre, programokra, megállapodásokra, illetve az a) és b) pontban meghatározottakra hatással lévő vagy valószínűleg hatással lévő tevékenységekre, valamint a környezet és a környezeti elemek védelmére hozott intézkedésekre és tevékenységekre;
-
a környezetvédelmi jogszabályok végrehajtásáról szóló jelentésekre;
-
a c) pontban említett intézkedések és tevékenységek keretein belül használt, költséghatékonysági és más gazdasági elemzésekre és feltevésekre;
-
az emberi egészség és biztonság állapotára - ideértve az élelmiszerlánc szennyeződését, az emberi életfeltételeket, a kulturális helyszíneket és építményeket - amennyiben azokra a környezeti elemek állapota vagy ezeken az elemeken keresztül a b) vagy c) pontban említett bármilyen tényező vagy intézkedés hatással van, vagy hatással lehet.
A környezeti információt lehetőség szerint elektronikus adatbázisokban kell nyilvántartani. A megfelelő szintű technikai feltételek rendelkezésre állása esetén a környezeti információt az adott szervezet hivatalos internetes honlapján is meg kell jeleníteni, a közölt adatok folyamatos frissítésével. Emberi egészséget vagy a környezetet érő közvetlen fenyegetés esetén – függetlenül attól, hogy emberi tevékenység vagy természeti ok idézi elő –, a környezeti információval rendelkező szerv a birtokában lévő vagy számára tárolt környezeti információt közzéteszi a várható kihatással érintett lakosság számára azonnal és késedelem nélkül, lehetővé téve a fenyegetésből származó kár megakadályozására vagy csökkentésére irányuló intézkedések megtételét.
Az Európai Közösségek Bizottsága a 96/23/EK tanácsi irányelvben rögzítette az analitikai módszerek elvégzése és az eredmények értelmezése terén használatos fogalmakat.
A precizitás, vagy pontosság (precision) a mérési eredményeknek az átlagérték körüli ingadozását kifejező mértékszám (önálló vizsgálati eredmények közeliségét mutatja meg). A pontosság növelhető a párhuzamosan elvégzett mérések számával.
A torzítás, helyesség vagy egzaktság (accuracy) a mérési eredmények átlagának valamilyen módon rögzített referenciaértéktől, valós értéktől való eltérése. A torzítás közvetlenül nem ismerhető fel a mérési eredményekből, és nem csökkenthető a vizsgálatok számának növelésével.
Az ismételhetőség azt mutatja meg, hogy ugyanazt a vizsgálati mintát, ugyanaz a személy, azonos körülmények esetén más alkalommal milyen pontossággal tudja megmérni.
A reprodukálhatóság pedig azt fejezi ki, hogy ugyanazt a vizsgálati mintát, azonos körülmények között más személy milyen precizitással méri meg.
„Egy mérés nem mérés, egy számítás önámítás” – tartja a mondás. Egy mérést, ha többször megismételünk, azt tapasztaljuk, hogy mérési eredményeink ingadoznak, szórnak. A megismételhetőség jól szemléltethető egy céltáblával (5.1 ábra). Van öt lehetőség lőni. Vajon a céltábla közepén lesznek-e a találatok? A méréstechnika nyelvén megfogalmazva: a mért érték (aktuális találat) mennyire közelíti meg a valódi értéket (célpontot)?
Egy kezdő (1) pontatlan, találatainak nagy a szórása: minél nagyobb a bizonytalanság, annál kisebb az ismétlőképesség; míg a profi (4) pontos és precíz: a valódi értékhez közeli és jó ismétlőképességű.
A csúcsnál van a legvalószínűbb (várható) érték: itt csoportosulnak a találatok, a széles terjedelem pedig a nagy bizonytalanságra utal (nagy szóródásra) utal (5.2 ábra). Ezek a görbék a várható érték (m = mean) és a pontosság mértékét jellemző szórás (σ) paraméterekkel le.
Méréseink tehát mindig hibásak, és eredményeink megítélése szempontjából rendkívül fontos a mérési hiba nagyságának, és típusának ismerete.
A hibaforrások közül a mérőeszközök tökéletlenségét, a kísérleti körülmények kismértékű változását (objektív hibák), és az érzékszerveink hibáját, a kísérletet végző személlyel kapcsolatos szubjektív tényezőket kell kiemelni. Az igen durva hibáktól eltekintve (mint pl. az eszközök helytelen használata, az eszköz/mérőműszer hibás leolvasása, vagy az adatok téves feljegyzése) a hibákat két nagy csoportba oszthatjuk:
1) Szisztematikus hibát okozhat a készülékek és eszközök pontatlansága, a kísérleti körülmények helytelen megválasztása, az eredmények helytelen értékelése. Ezek egy méréssorozatban minden eredményt azonos mértékben és irányban befolyásolnak (torzítanak), ezért nehéz ezeket a hibaforrásokat felfedezni. A valódi érték és a mért adatok átlagának eltérése adja a mérés torzítását (céltábla második ábrája és az alábbi 5.3 ábra illusztrálja a torzítást).
A torzítást a mérések átlagának (xátlag) a valós értéktől (xvalós) való eltérése jellemzi. Számszerű adatát a mérés során akkor lehet meghatározni, ha ismert a valós érték (referencia, vagy irodalmi adat). Az abszolút érték százalékában relatív hibaként szokták kifejezni (accuracy %):
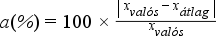
2) Véletlen hibák a véletlen megfigyelési és leolvasási hibákból, az objektív és szubjektív kísérleti feltételek kismértékű, ellenőrizhetetlen ingadozásából, egyes műveletek helytelen kivitelezéséből származnak. Ezek szabják meg a vizsgálat pontosságát, hogy a mérési eredmények mennyire térnek el a középértéktől (milyen a mérés szórása), valamint az eredmény megismételhetőségét és reprodukálhatóságát. A véletlen hibák nagysága több párhuzamos mérés elvégzésével csökkenthető, mivel a számtani átlagban a hibák kompenzálják egymást. Kis pontosság esetén az egyes eredmények jelentős az eltérést mutatnak az átlagtól (céltábla harmadik ábrája és a 5.4 ábra mutatja be a jelenséget).
A pontosság mértékének megállapítására a szórás (s) számítását alkalmazzuk, amellyel a mért adatoknak az átlagtól való eltérését jellemezzük. Az egyes mérési eredmények átlagtól való eltérésének négyzetösszegét osztjuk a mérések számával, majd négyzetgyököt vonunk.
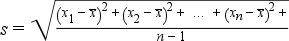
A pontosságot az átlag ± szórás alakban adhatjuk meg (Δ = xátlag ± s), vagy a mérés százalékos relatív hibájaként (δ % = 100 · s / xátlag).
Tartalom
Főként nagy mennyiségű adatok gyűjtése, és azok számítógépen történő regisztrálása során jelentkező hibát mutatunk be az alábbiakban. Előfordulhat, hogy egy-egy mérőberendezés valami okból kifolyólag leáll, majd automatikusan újraindul. Ilyen esetekben ezeket az értékeket ki kell szűrni (6.1 ábra, a sárgával jelölt rész törlendő), és törölni kell az adatbázisból a további feldolgozás előtt, ugyanis az adatbázis kezelő rendszerek nem képesek figyelmen kívül hagyni az érvénytelen adatokat.
A 6.2 ábra szereplő adatsor az Észak-dunántúli Környezetvédelmi Felügyelőség adatbázisából származik, a győri és esztergomi levegőtisztaság-védelmi mérőkonténerek regisztrálták. A szálló por PM10 és PM2,5-es frakcióit mutatja az ábra. A PM10 a 10 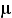 ;m átmérőnél kisebb részecskéket jelenti, míg a PM2,5 a 2,5
;m átmérőnél kisebb részecskéket jelenti, míg a PM2,5 a 2,5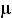 m-nél kisebbeket. Tekintettel arra, hogy a PM2,5 a PM10 részét képei, így nem lehet nagyobb az előbbi érték az utóbbinál. Tehát a szűrés nem feltételül merül ki csak az érvénytelen adatok kiszűrésében, előfordulhat, hogy további vizsgálatokat is kell végezni. A központi – online elérhető – adatbázisokból az ilyen típusú hibákat nem minden esetben távolítják el.
m-nél kisebbeket. Tekintettel arra, hogy a PM2,5 a PM10 részét képei, így nem lehet nagyobb az előbbi érték az utóbbinál. Tehát a szűrés nem feltételül merül ki csak az érvénytelen adatok kiszűrésében, előfordulhat, hogy további vizsgálatokat is kell végezni. A központi – online elérhető – adatbázisokból az ilyen típusú hibákat nem minden esetben távolítják el.
A mérési eredmények/adatok feldolgozásra történő előkészítése során, továbbá azok kiértékelési folyamataiban számos esetben találkozunk statisztikából ismerős fogalmakkal, összefüggésekkel. Az összes lehetséges esetet lehetetlen lenne itt felsorolni, de a leggyakrabban előforduló fogalmakat az alábbi fejezetben bemutatjuk. Egy rövid elméleti áttekintés után, mindenhol egy általunk választott/megoldott példán keresztül mutatjuk be azok gyakorlati alkalmazását.
Számtani közép: az összes mérési eredmény figyelembe vételével számolt átlagérték.
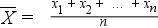
Pontosság: a középérték 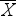 és a pontos érték X0 különbsége a pontos értékre vonatkoztatva.
és a pontos érték X0 különbsége a pontos értékre vonatkoztatva.
Adatok szórása: az egyes mérési eredményeknek a középértéktől való eltérését mutatja. Definíciója szerint az adatok 2/3-ad része az 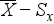 és
és 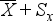 közötti tartományban található.
közötti tartományban található.
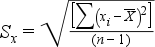
Szórásnégyzet (variancia): az adatok és a középértékek közötti eltérések négyzeteinek középértéke (Sx2)
Középérték szórása (standard hiba): a középérték megbízhatóságának jellemzésére szolgál.
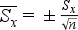
Változási együttható (variációs koefficiens): az adatok százalékos szórására ad felvilágosítást.
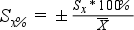
Középérték százalékos hibája (relatív hiba): az eredmények kiírható számjegyeinek számát ez alapján határozzuk meg.
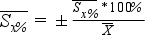
Példa: Titrimetriás meghatározásnál a hallgatók által mért fogyások a következők: 0,98 cm3; 0,78 cm3; 0,90 cm3; 0,94 cm3; 0,96 cm3; 0,98 cm3; 0,94 cm3; 1,00 cm3; 1,12 cm3; 1,05 cm3; 0,98 cm3; 1,02 cm3; 0,92. A pontos érték 1,00 cm3 lett volna. Határozzuk meg a hibaszámítási adatokat.
7.1. táblázat - Hibaszámítási adatok – feladat megoldása
|
1 |
B |
C |
D |
E |
|---|---|---|---|---|
|
2 |
Mért fogyás |
Hibaszámítási adat |
Eredmény |
Érték |
|
3 |
0,98 |
Pontos középérték (cm3) |
1,00 |
- |
|
4 |
0,78 |
1 Adatok száma (db) |
13,00 |
- |
|
5 |
0,90 |
2 Átlag (cm3) |
0,98 |
- |
|
6 |
0,94 |
3 Adatok szórása (szórás) |
0,08 |
0,98 cm3 ± 0,08 cm3 |
|
7 |
0,96 |
4 Átlag szórása (standard hiba) |
0,02 |
0,98 cm3 ± 0,02 cm3 |
|
8 |
0,98 |
5 Variancia |
0,01 |
- |
|
9 |
0,94 |
6 Variációs koefficiens |
8,06 |
0,98 cm3 ± 8,06% |
|
10 |
1,00 |
7 Átlag százalékos hibája (relatív hiba) |
2,31 |
0,98 cm3 ± 2,31% |
|
11 |
1,12 |
8 Pontosság |
3,31 |
1,00 cm3 ± 3,30% |
|
12 |
1,05 | |||
|
13 |
0,98 | |||
|
14 |
1,02 | |||
|
15 |
0,92 | |||
| 1D4=DARAB(B3:B15) | 2D5=ÁTLAG(B3:B15) | 3D6=SZÓRÁS(B3:B15) | 4D7=D5/(HATVÁNY(D3;0,5)) |
| 5D8=VAR(B3:B15) | 6D9=(D6*100)/D3 | 7D10=(D7*100)/D5 | 8D11=((D3-D5)*100)*D3 |
Az egymintás próbák során az adathalmaz alapján becsült és az elméleti középérték, illetve szórások összehasonlítását végezzük. Amikor valamely adathalmaz becsült középértékének 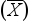 és az elméleti középértékének (X0) a különbözőségét akarjuk eldönteni a Student-féle egymintás t-próbát alkalmazzuk. Ilyenkor a
és az elméleti középértékének (X0) a különbözőségét akarjuk eldönteni a Student-féle egymintás t-próbát alkalmazzuk. Ilyenkor a 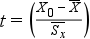 képlet segítségével kiszámítjuk az adathalmazra jellemző t-értéket, melyet összehasonlítunk a Student-próba táblázatban szereplő kiválasztott hibavalószínűségének (általában P=5%) és DF=n-1 szabadsági foknak megfelelő t-értékkel. Ha a számított t-érték nagyobb, mint a táblázatban szereplő kritikus érték, a megengedhető P hibavalószínűségi szinten szignifikánsan különbözőnek tekintjük a becsült és az elméleti középértéket.
képlet segítségével kiszámítjuk az adathalmazra jellemző t-értéket, melyet összehasonlítunk a Student-próba táblázatban szereplő kiválasztott hibavalószínűségének (általában P=5%) és DF=n-1 szabadsági foknak megfelelő t-értékkel. Ha a számított t-érték nagyobb, mint a táblázatban szereplő kritikus érték, a megengedhető P hibavalószínűségi szinten szignifikánsan különbözőnek tekintjük a becsült és az elméleti középértéket.
Példa: Egy mérőoldat koncentrációja 0,2 M volt készítéskor. Bizonyos idő eltelte után a töménységet újból ellenőriztük: 0,1968; 0,1950; 0,2018; 0,1938; 0,1944 M. Megváltozott-e a mérőoldat összetétele?
7.2. táblázat - Egymintás t- próba – feladat megoldása
|
adatok (M) |
0,1967 |
|
0,1895 | |
|
0,195 | |
|
0,2018 | |
|
0,1938 | |
|
0,1944 | |
|
átlag |
0,1952 |
|
szórás |
0,0040 |
|
átlag szórása |
0,0016 |
|
t-számított |
2,9223 |
|
elemszám |
6 |
|
t-érték (leolvasott: P=5%; DF=n-1=5) |
2,571 |
Következtetés: mivel a 6.2 táblázatban számított t-érték nagyobb, mint a 4.6. melléklet táblázatban szereplő kritikus érték, elmondható, hogy az oldat összetétele szignifikánsan megváltozott, a megengedhetőnél nagyobb mértékben.
A környezeti elemek (tulajdonságai időben gyakran változnak. Az adatok nagy szórása ellenére is értékelnünk kell a mérési eredményeket úgy, hogy azok a környezeti elem változására legyenek jellemzőek. Ezt úgy valósítjuk meg, hogy a vizsgált jellemző gyakoriságát és kumulatív gyakoriságát elemezzük. A gyakorisági adatokat hisztogram segítségével szemléltetjük.
Gyakoriság vizsgálatakor arra vagyunk kíváncsiak n számú mérési adat esetében, hogy ezek közül egy adott „A” mérési tartományon (osztályon) belül hány mérési adatunk (K) szerepel. „K” értékét, azaz az egy osztályba tartozó mérési adatok számát osztálygyakoriságnak nevezzük.
A kumulatív gyakoriság (összegzett gyakoriság, tartósság) tulajdonképpen a gyakoriság integrálja, vagyis a görbe alatti területtel egyenlő.
Példa: Dolgozzuk fel egy nagyváros levegőjének SO2 szennyezettségére vonatkozó adatsorát. Határozzuk meg a szükséges paramétereket a relatív és az összetett gyakorisági eloszláshoz egyaránt.
7.3. táblázat - A feladat megoldása – 1. rész
|
Napok |
SO2 konc (µg/m3) |
Rendezett adatsor |
Osztályköz megállapításához használt osztó javasolt értékei | |
|---|---|---|---|---|
|
1 |
21,4 |
5,0 |
Adatok száma (n) |
Osztó ( C ) |
|
2 |
9,7 |
5,0 |
0 |
3,7 |
|
3 |
10,8 |
6,5 |
30 |
4,1 |
|
4 |
14,3 |
8,0 |
50 |
4,5 |
|
5 |
20,6 |
8,4 |
75 |
4,8 |
|
6 |
20,2 |
9,1 |
100 |
5 |
|
7 |
10,9 |
9,3 |
150 |
5,3 |
|
8 |
5,0 |
9,6 |
200 |
5,5 |
|
9 |
10,1 |
9,7 |
300 |
5,8 |
|
10 |
14,5 |
10,1 |
400 |
5,9 |
|
11 |
18,9 |
10,8 |
500 |
6,1 |
|
12 |
20,2 |
10,9 |
700 |
6,3 |
|
13 |
12,5 |
10,9 |
1000 |
6,5 |
|
14 |
17,2 |
12,5 | ||
|
15 |
16,1 |
12,7 |
Adatok száma (n) |
30,0 |
|
16 |
14,5 |
13,1 |
Minimum (Xmin) |
5,0 |
|
17 |
9,6 |
14,3 |
Maximum (Xmax) |
41,5 |
|
18 |
16,7 |
14,5 |
Átlag |
14,2 |
|
19 |
16,8 |
14,5 |
Variáció szélesség (W=Xmax-Xmin) |
36,5 |
|
20 |
13,1 |
16,1 |
Osztó értéke ( C ) |
4,1 |
|
21 |
9,3 |
16,7 |
Szórás közelítő értéke (S'=W/C) |
8,9 |
|
22 |
12,7 |
16,8 |
Osztályköz értéke (A=S'/4) |
2,2 |
|
23 |
21,2 |
17,2 | ||
|
24 |
41,5 |
18,9 | ||
|
25 |
10,9 |
20,2 | ||
|
26 |
5,0 |
20,2 | ||
|
27 |
6,5 |
20,6 | ||
|
28 |
9,1 |
21,2 | ||
|
29 |
8,4 |
21,4 | ||
|
30 |
8,0 |
41,5 | ||
A 6.3 táblázat adatsorai alapján elkészíthetjük a kén-dioxid adott hónapra jellemző 24 órás értékeiből álló vonaldiagramját 6.3 ábra.
A feladat megoldása során elkészítünk egy osztálybeosztást (koncentráció tartomány oszlop), majd meghatározzuk az egyes osztályokba tartozó elemek számát (gyakorisági adatok száma). Az Excel „gyakoriság” függvényének segítségével számítjuk ki a gyakorisági adatok számát (6.4 táblázat).
7.4. táblázat - A feladat megoldása – 2. rész
|
Konc. tart. A |
Gyakorisági adatok száma K |
Relatív gyakoriság K/n |
Relatív gyakoriság (%) K/n (%) |
Konc. tart. A |
Kumulatív Gyakorisági adatok száma K |
Kumulatív Relatív gyakoriság K/n |
Kumulatív Relatív gyakoriság (%) K/n (%) |
|---|---|---|---|---|---|---|---|
|
2 |
0 |
0,000 |
0,00 |
2 |
0 |
0,000 |
0,00 |
|
4 |
0 |
0,000 |
0,00 |
4 |
0 |
0,000 |
0,00 |
|
6 |
2 |
0,067 |
6,67 |
6 |
2 |
0,067 |
6,67 |
|
8 |
2 |
0,067 |
6,67 |
8 |
4 |
0,133 |
13,33 |
|
10 |
5 |
0,167 |
16,67 |
10 |
9 |
0,300 |
30,00 |
|
12 |
4 |
0,133 |
13,33 |
12 |
13 |
0,433 |
43,33 |
|
14 |
3 |
0,100 |
10,00 |
14 |
16 |
0,533 |
53,33 |
|
16 |
3 |
0,100 |
10,00 |
16 |
19 |
0,633 |
63,33 |
|
18 |
4 |
0,133 |
13,33 |
18 |
23 |
0,767 |
76,67 |
|
20 |
1 |
0,033 |
3,33 |
20 |
24 |
0,800 |
80,00 |
|
22 |
5 |
0,167 |
16,67 |
22 |
29 |
0,967 |
96,67 |
|
24 |
0 |
0,000 |
0,00 |
24 |
29 |
0,967 |
96,67 |
|
26 |
0 |
0,000 |
0,00 |
26 |
29 |
0,967 |
96,67 |
|
28 |
0 |
0,000 |
0,00 |
28 |
29 |
0,967 |
96,67 |
|
30 |
0 |
0,000 |
0,00 |
30 |
29 |
0,967 |
96,67 |
|
32 |
0 |
0,000 |
0,00 |
32 |
29 |
0,967 |
96,67 |
|
34 |
0 |
0,000 |
0,00 |
34 |
29 |
0,967 |
96,67 |
|
36 |
0 |
0,000 |
0,00 |
36 |
29 |
0,967 |
96,67 |
|
38 |
0 |
0,000 |
0,00 |
38 |
29 |
0,967 |
96,67 |
|
40 |
0 |
0,000 |
0,00 |
40 |
29 |
0,967 |
96,67 |
|
42 |
1 |
0,033 |
3,33 |
42 |
30 |
1,000 |
100,00 |
|
Össz |
30 |
1,000 |
100,00 | ||||
A relatív gyakoriság és a relatív %-os gyakoriság oszlopok kitöltése után megrajzolhatók a gyakorisági eloszlás és kumulált gyakorisági eloszlás függvényeink (6.4 ábra és 6.5 ábra).
Példa: Egyik munkánk során Veszprémben szálló por mintavételezést végeztük 4 helyszínen (6.6. ábra) elsődlegesen olyan meggondolásból, hogy meghatározhassuk, a járműforgalommal különbözőféleképpen terhelt területeken a PM10-ben milyen arányt képvisel a PM2,5 frakció. A mérési sorozatok megkezdése előtt a két – mérések során alkalmazott – mintavevővel párhuzamos méréseket végeztünk (azonos előleválasztó fejeket használva, 6.5 és 6.6. táblázat), annak megállapítására, hogy a mérések során kapott eredmények mennyiben felelnek meg a pontossági kritériumoknak.
Elvégeztük a 95%-os megbízhatósági szinthez tartozó statisztikai vizsgálatokat, a számítási eredmények alapján pedig megállapítható volt, hogy a két féle előleválasztó fejjel végzett párhuzamos összemérésekre kiszámolt K95 konfidencia intervallumok[3] teljesítik a mérések pontosságával kapcsolatos előírásokat, azaz K95 ≤ 5 µg/m3.
7.5. táblázat - PM10 - párhuzamos mérések eredményei
|
Készülék / Minta azonosító |
Dátum/Idő |
t [h] |
p [mbar] |
T [°C] |
V [m3] |
V0 * [m3] |
mpor [mg] |
c* [µg/m3] | |
|---|---|---|---|---|---|---|---|---|---|
|
indul-leáll | |||||||||
|
861 |
P1 |
szept.04 16:00 szept.05 16:00 |
24 |
957 |
25,6 |
754,2 |
699,2 |
10,0 |
14,3 |
|
861 |
P2 |
szept.05 16:00 szept.06 16:00 |
24 |
958 |
26,8 |
755,3 |
698,0 |
12,9 |
18,5 |
|
861 |
P3 |
szept.06 16:00 szept.07 16:00 |
24 |
954 |
28,4 |
758,9 |
694,7 |
29,3 |
42,2 |
|
963 |
P4 |
szept.04 16:00 szept.05 16:00 |
24 |
958 |
25,4 |
753,6 |
699,8 |
9,5 |
13,6 |
|
963 |
P5 |
szept.05 16:00 szept.06 16:00 |
24 |
954 |
26,9 |
757,0 |
696,5 |
13,4 |
19,2 |
|
963 |
P6 |
szept.06 16:00 szept.07 16:00 |
24 |
954 |
28,4 |
758,9 |
694,7 |
28,9 |
41,6 |
*293K hőmérsékletre; 1,013kPa nyomásra átszámítva
7.6. táblázat - PM2,5 - párhuzamos mérések eredményei
|
Készülék / Minta azonosító |
Dátum/Idő |
t [h] |
p [mbar] |
T [°C] |
V [m3] |
V0 * [m3] |
mpor [mg] |
c* [µg/m3] | |
|---|---|---|---|---|---|---|---|---|---|
|
indul-leáll | |||||||||
|
861 |
P7 |
okt.27 15:00 okt.28 15:00 |
24 |
944 |
13,9 |
706,0 |
708,4 |
50,9 |
71,9 |
|
861 |
P8 |
okt.28 15:00 okt.29 15:00 |
24 |
942 |
15,5 |
709,3 |
705,6 |
29,3 |
41,5 |
|
861 |
P9 |
okt.29 15:00 okt.30 15:00 |
24 |
937 |
16,8 |
711,9 |
702,2 |
10,7 |
15,3 |
|
963 |
P10 |
okt.27 15:00 okt.28 15:00 |
24 |
944 |
14,2 |
708,5 |
708,1 |
50,5 |
71,3 |
|
963 |
P11 |
okt.28 15:00 okt.29 15:00 |
24 |
942 |
15,9 |
711,2 |
705,1 |
29,2 |
41,4 |
|
963 |
P12 |
okt.29 15:00 okt.30 15:00 |
24 |
935 |
17,7 |
713,7 |
700,3 |
10,9 |
15,6 |
* 293K hőmérsékletre; 1,013kPa nyomásra átszámítva
Látható, a következő . táblázatban, hogy a K95 konfidencia intervallumok mindkét esetben teljesítik a pontossággal kapcsolatos előírásokat (K95 ≤ 5 µg/m3).
7.7. táblázat - Statisztikai vizsgálatok eredménye
|
Párhuzamosan mért minták jele |
Di (µg/m3) (különbség) |
Di2 (µg/m3)2 |
Di2 /2n |
∑Di2 /2n |
Sa |
K95 |
|---|---|---|---|---|---|---|
|
|P1-P4| |
0,7 |
0,49 |
0,082 |
PM10 | ||
|
|P2-P5| |
0,7 |
0,49 |
0,082 |
0,223 |
0,47 |
2,03 |
|
|P3-P6| |
0,6 |
0,36 |
0,060 | |||
|
|P7-P10| |
0,6 |
0,36 |
0,060 |
PM2,5 | ||
|
|P8-P11| |
0,1 |
0,01 |
0,002 |
0,077 |
0,28 |
1,20 |
|
|P9-P12| |
0,3 |
0,09 |
0,015 | |||
Vannak esetek, amikor egy adathalmazról el kell döntetnünk, hogy a kiugrónak vélt adatokat kizárjuk-e, vagy figyelembe vegyük a számításoknál. Több módszer is létezik az ilyen vizsgálatokra, mint például a Dixon-féle r-próba, a Nalimov-próba, illetve a jelen esetben bemutatott – legegyszerűbb és leggyorsabb – Z-próba.
Példa: Egy adatsor a következő elemekből áll: 9, 10, 14, 8, 11, 20, 11, 8, 3, 10, 11. Kizárjuk-e a kiugrónak vélt 3-as és 20-as adatokat az átlagszámításból?
Standardizálással oldható meg a feladat a legegyszerűbben.
Lehetőség van Excel programban standardizálásra és a kritikus Z érték meghatározására. Standardizálás: Normalizálás(X;középérték;szórás), mely középértékkel és szórással megadott adatokból standardizált (normalizált) értéket ad eredményül, vagyis a számított Z értéket. A kritikus Z érték: Storneloszl(X), mely a standardizált normáleloszlás értékét számítja ki, így használható a kritikus Z értéket tartalmazó táblázat helyett.
7.8. táblázat - Feladat megoldása standardizálással
|
adatok |
3 |
|
8 | |
|
8 | |
|
9 | |
|
10 | |
|
10 | |
|
11 | |
|
11 | |
|
11 | |
|
14 | |
|
20 | |
|
átlag |
10,45 |
|
szórás |
4,18 |
|
Z(max)=(Xmax-Xátl)/Sx |
2,28 |
|
Z(min)=(Xmin-Xátl)/Sx |
-1,78 |
Akkor tekintenénk az értékeket kiugrónak jelen példában a Z próba alapján, ha ± 3 értéken kívül esne. Ez a feltétel nem teljesül, tehát nem kiugró értékek jelen vizsgálati módszer alapján.
[3] Ismert paraméterű mintából következtetünk az ismeretlen paraméterű alapsokaságra. Az alkalmazásokban legtöbbször 95%-os megbízhatósági szintű konfidencia-intervallumokat használnak.
A mérőeszközöket, műszereket jellemezhetjük azok leolvasási pontosságával. Vegyük példának a mérlegeket. Beszélhetünk táramérlegről, vagy éppen a pontosabb eredményeket mutató analitikai mérlegről. A megfelelő választást a vizsgálat célja határozza meg.
Példa: Adott egy gravimetriás módszerrel meghatározandó porminta (7.1 ábra). A mintát egy nagytérfogatú pormintavevő segítségével vesszük. Adott térfogatárammal levegőt szívatunk át a rendszeren, és a „levegő útjába” szűrőpapírt teszünk. A szűrőpapírt (szabványban meghatározott módon) klimatizált mérlegszobában a mintavétel előtt üresen, és a mintavételezés után is lemérjük. A kettő különbsége adja a mérési időintervallumra jellemző por tömegét. A tömegeket minden esetben korrigálni kell a referencia szűrőpapírunk tömegváltozásával. Rendkívüli pontosságot megkövetelő mérési folyamatról révén szó, ebben az esetben alapkövetelmény, hogy mérlegünk négy tizedes jegy pontosságig legyen képes eredményt szolgáltatni.
Felesleges nagy érzékenységű analitikai mérleget használnunk például akkor, ha valamilyen reagens-oldatot készítünk, amit aztán mérőhengerrel adunk a vizsgálandó anyaghoz. Fontos szem előtt tartani a mérőműszerek mérési tartományát is, hogy azok a vizsgálat céljának megfeleljenek.
A mintavétel módja és helyszíne minden esetben függ a vizsgálat céljától, a szennyezés jellegétől, kiterjedésétől, illetve hogy milyen típusú mintavételezésről van szó (on-line[4] , in-line [5] , vagy off-line [6] ). Ezek figyelmen kívül hagyása esetén a mintánkra vonatkozó eredmények nem lesznek reprezentatívak. A helyszíntől távol vizsgálandó minták esetében (off-line) figyelemmel kell lenni a minták tartósítására, szállítására és tárolására. A vonatkozó szabványok részletes leírást adnak minden mintavételezéssel és vizsgálattal kapcsolatos tevékenységről, előírásokról.
Vízmintavétel esetében például fontos szem előtt tartani, hogy a levegővel történő érintkezés megváltoztathatja a minta tulajdonságait. A vízminőség legtöbb esetben helyileg és térben is változik, tehát rendszerint sorozatos mintavétel szükséges. Felszín alatti vizek mintavételezése esetén (monitoring kútból) nem a kútban összegyűlt vizet vizsgáljuk, hanem a kútban lévő víz mennyiségének háromszorosát először kitermeljük, és az utána, a földtani közegből helyére áramló vízből kell a mintát venni. A mintatároló edényre vonatkozóan is vannak követelmények, a víz szerves komponenseinek vizsgálatához rendszerint üvegből, szervetlen komponenseinek analíziséhez pedig műanyagból készült palackot kell használni, mintával ezeket túl kell tölteni, és légmentesen szállításhoz lezárni
Földtani közeg vizsgálatánál lehetőleg genetikai szintenként kell mintázni. A művelt felső réteget a művelés mélységéig (0-20 vagy 0-30 cm), a bolygatatlan altalajt általában 30 cm-enként. A vizsgálatok jellegéből, céljából adódóan azonban a mintavételi mélység változhat. Szennyezett területen, pl. gyárudvaron, gyakran több méter mélységben nem talaj a takaró réteg, hanem salak vagy iszapok, egyéb üzemi hulladék. Szennyezés esetén a transzportfolyamatokat a földtani közeg szerkezete jelentősen befolyásolja.
Levegőtisztaság-védelem területén is megvannak a követelmények a mintavételezés reprezentatív kivitelezéséhez. Immissziós telepített/mobil mérőállomások esetén a mintavételi magasság 3-5 m magasságban legyen, a mintavevő beszívó nyílásait és a meteorológiai árbocot környezeti tárgyak ne zavarják (épületek, fák), és helyükről a szabad égbolt legalább 45° alatt látható legyen minden irányban. Az állomás jó átszellőzésű legyen, és nem lehet szennyező forrás közvetlen közelében. Ez utóbbi miért fontos? A várpalotai mérőkonténer a város egyik legforgalmasabb útszakasza mellett van telepítve. Ennek köszönhetően téli (fűtési) időszakban a szükségesnél gyakrabban kell elrendelni szmog riadót a megnövekedett szálló por koncentráció miatt.
Az adatbázis többnyire strukturált adatok összessége, amelyet egy tárolására, lekérdezésére és szerkesztésére alkalmas szoftvereszköz kezel. Ezek közül ma már egyre inkább az osztott adatbázisok jelentősége nőtt meg.
Az osztott adatbázisok létrehozásának célja több irányba is mutat. E célok lehetnek:
-
minél nagyobb adatelérési sebesség biztosítása – például a GRID típusú hálózatok alkalmazása esetén;
-
megosztott munkavégzés (ide értve nem csak a gépek számítási kapacitását, hanem az emberi erőforrásokat is)
-
megnövelt adatbiztonság
-
a legjobb tároló hely kihasználtság biztosítása
E célok megvalósítását a következő példák szemléltetik.
Az elmúlt évek legígéretesebb informatikai fejlesztési iránya a GRID rendszerek irányába mutatott. Az elképzelés alapja, hogy a mai számítógépek számítási teljesítménye – és sok esetben tárolási is – jelentősen meghaladja a hétköznapi felhasználáshoz szükséges értéket. Tipikus példa erre az adminisztrációs számítógépek, amelyek, melyek a tapasztalatok alapján átlagosan legfeljebb 30%-t használják ki a rendszer számítási teljesítményének. A nem használt teljesítmény kihasználásával több nagy számításigényű alkalmazást sikerült világszerte megvalósítani. Az első szakmailag igen sikeres – bár a célját eddig el nem érő – kísérlet a SETI@Home rendszere volt, amit a Berkeley Egyetem fejlesztett és tart fent a mai napig. E rendszerben a legjobb időszakban 1,5 millió számítógép dolgozott egyszerre.
A siker hatására számos egyéb területre elkezdték fejleszteni a GRID-es alkalmazásokat, így nemsokára megjelentek az adatbázis kezelés területén, majd megalkották az Open Grid Services Architecture-t, amely jelentősen megkönnyítette a fejlesztési munkákat.
A térinformatika területén szintén a számítási teljesítmény minél jobb kihasználása volt az elsődleges cél, de itt már megjelenik a nagy méretű adatbázisok felosztásának az igénye is.
Az adatbázisok megosztása esetén kiemelt szempont lehet az adatok biztonsága. Egy adatbázis felépítése és karbantartása ma már lényegesen nagyobb értéket képvisel egy rendszer összértékében, mint 15-20 évvel ezelőtt (8.1 ábra). Ezen felül, míg egy szoftver vagy hardver elemet újra elő lehet állítani, az adatra ez legtöbbször nem igaz. Ezért egyre fontosabb az adatok biztonsága.
9.1. ábra - A hardver, szoftver és az adat árainak egymáshoz viszonyított aránya a számítástechnika korai korszakában és ma
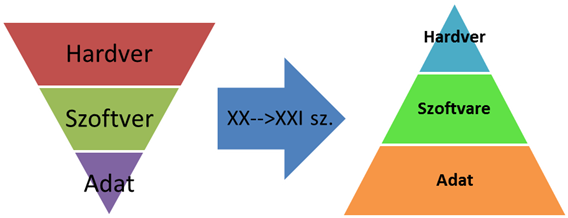 |
Ezt az adatvédelmi igényt meg lehet oldani folyamatos mentési rendszer felállításával. Ez régebben egyszerű mentésekkel oldották meg (például minden éjszaka), amit később kiegészített a mentett adatok folyamatos tükrözése (például RAID1 vagy RAID5 szervezésű meghajtók üzembe állításával). Ezeknek a módszereknek közös hátrányuk volt, hogy jellemzően fizikailag közel tárolták egymáshoz az éles és a mentett adatokat, ami egy szerencsétlenség vagy egyéb nem várt esemény bekövetkeztekor gyakran járt teljes adatvesztéssel. A széles sávú internet megjelenésével lehetségessé vált a mentések és az éles adatok földrajzilag történő elkülönítése.
A földrajzi elkülönítés klasszikus formája a teljes adatállomány teljes átmásolása a világ más pontján lévő biztonsági tározóra. Ez azonban nagy méretű adatbázisok esetén – még a korszerű tömörítési módszerek ellenére is – igen időigényes volt. Erre hozott megoldást az osztott adatbázisok használata, amelyet ötvöztek a 90’ évek végén – igaz más okokból – népszerűvé vált Peer-To-Peer (P2P) technikájával.
A kialakított megoldás alapgondolata a következő ábrasorral szemléltethető. Egy 10 TiB méretű adatbázis hardver oldali felépítése klasszikus módon a következő (8.2 ábra):
Az osztott adatbázisok egyrészt logikailag feldarabolva az adatbázist lecsökkentik a részek méretét – bár sok esetben megnövelik az összes méret – így lehetővé válik, hogy minden rész önálló, kisebb méretű, olcsóbban beszerezhető és fenntartható tárhelyen helyezkedjék el. Ez egyben segíti az adatlekérdezéshez kötődő sávszélesség legjobb kihasználását is. (8.3 ábra)
A legkorszerűbb és igen költséghatékony rendszerek jellemzően nem használnak helyi fizikai tükrözést, hanem adatbázis-szegmensenként legalább három számítógép között P2P kapcsolattal folyamatosan biztosítják a gépeken lévő tartalom szinkronizálását. Ez esetben jellemzően mindhárom gép képes adatszolgáltatásra is, ami nagy mértékben megnöveli a lekérdezések válaszsebességét – főleg konkurens felhasználói környezetben. Biztonsági okokból e rendszerekről is készül időnként teljes adatbázismentés, ami egy a szándékos – emberi – beavatkozásra történő adatvesztés kivédésére szolgál. E korszerű rendszerek felépítését alább láthatjuk (8.4 ábra)
Tartalom
Mért adataink gyors áttekintésének módszere a grafikus ábrázolás, végeredménye pedig a grafikon. A grafikonos ábrázolás-technikai eszközei mértani elemek: pont, vonal, téglalap, kör, továbbá ezek kombinációi, így ennek megfelelően beszélhetünk pont-, vonal-, terület- és síkdiagramról.
A grafikus ábrázolás módját, eszközét mindig az elérni kívánt cél határozza meg. A mérések számától, illetve a vizsgált változó jellegétől függően különböző ábrázolási módok alkalmazhatók. Néhány speciális grafikus ábra (mint a dobozdiagram és a szár-levél diagram) csak kimondottan statisztikai programok segítségével készíthető el (SPSS), de a legtöbb – a manapság már minden számítógép használó számára elérhető – Excel program segítségével is létrehozható.
A diagramtípus alkalmazási módjának szemléletes bemutatására nézzünk meg egy példát. Készítsünk el a vizsgált mintavételi helyre jellemző összessó-tartalom csillagábrát a megadott adatok alapján.
10.1. táblázat - Vizsgált mintavételi helyre jellemző összessó-tartalom jellemző és számított adatsorai
|
mg/l |
egyenérték súly |
mg- egyenérték |
egyenérték % S |
a (cm) |
2,6 |
2,6 | |||
|---|---|---|---|---|---|---|---|---|---|
|
K+ |
0 |
39,098 |
0 |
0 |
0 |
2,6 |
0 |
K+ | |
|
Na+ |
2 |
22,99 |
0,87 |
1,22 |
0,1 |
2,6 |
2,6 | ||
|
Ca2+ |
101,2 |
20,04 |
5,05 |
70,68 |
7,4 |
2,6 |
0,1 |
Na+ | |
|
Mg2+ |
24,4 |
12,152 |
2,008 |
28,1 |
2,9 |
2,6 |
2,6 | ||
|
∑kation |
- |
- |
7,145 |
100 |
- |
2,6 |
7,4 |
Ca2+ | |
|
SO42- |
10 |
48,029 |
0,208 |
1,51 |
0,2 |
2,6 |
2,6 | ||
|
Cl- |
0,5 |
35,453 |
0,014 |
0,1 |
0 |
2,6 |
2,9 |
Mg2+ | |
|
HCO3- |
555 |
61,017 |
9,096 |
65,83 |
6,9 |
2,6 |
2,6 | ||
|
CO32- |
135 |
30,005 |
4,499 |
32,56 |
3,4 |
2,6 |
0,2 |
SO42+ | |
|
∑anion |
- |
- |
13,817 |
100 |
- |
2,6 |
2,6 | ||
|
∑ |
- |
- |
20,962 |
- |
- |
2,6 |
0 |
Cl- | |
|
621 µS/cm |
sugár r |
2,6 |
2,6 |
2,6 | |||||
|
2,6 |
6,9 |
HCO3- | |||||||
|
2,6 |
2,6 | ||||||||
|
2,6 |
3,4 |
CO32- | |||||||
El kell készíteni a táblázat első fele alapján a poláris diagramunk adattábláját (utolsó 3 oszlop, 9.1 táblázat. Vizsgált mintavételi helyre jellemző összessó-tartalom jellemző és számított adatsorai), majd a diagramvarázsló sugár-diagram típusának kiválasztásával elkészíthető az alábbi, 9.1 ábra.
Az ábráról leolvasható, hogy a legnagyobb részesedésű a kationok közül a Ca2+, az anionok közül pedig a HCO3-.
A pontdiagram és a vonaldiagram nagyon hasonlít egymásra, különösen, ha a pontdiagramon az összekötő vonalak is fel vannak tüntetve. Egy formázott pontdiagram számértékeket jelenít meg a vízszintes és a függőleges tengely mentén; az értékeket pedig az adatpontokban egyesíti. Ezzel szemben a formázott vonaldiagram a kategóriaadatokat (jelen esetben időközöket) a vízszintes tengely mentén, a számértékeket pedig a függőleges tengely mentén egyenletesen elosztja.
Tehát pont- és a vonaldiagram között az a legfőbb különbség, ahogyan az adatokat a tengelyeken ábrázoljuk. Ha például a 9.2 ábrán szereplő munkalapadatok alapján készítünk egy pont- és egy vonaldiagramot, látható, hogy az adatok elosztása eltérő lesz a két esetben (9.3. ábra.).
Egy vagy több adathalmazból képezett görbe által lefedett terület megjelenítését szolgálja (9.4 ábra). Vonal-, illetve pontdiagramnál látványosabb prezentációját szolgálja az adatoknak.
A kördiagram és a perecdiagram is a részek egészhez való viszonyát tükrözi, a perecdiagram ugyanakkor több adatsort is tartalmazhat egyszerre.
A perec diagram lehetőséget biztosít több adatsor egyidejű összehasonlítására (9.6 ábra). Az előző ábrán látható 2010-es statisztikai adatokat összehasonlíthatjuk például korábbi évek statisztikai adataival. Példánk esetében a 2008-as és 2010-es évet vizsgáltam.
10.6. ábra - Földhasználat művelési ágak szerint (2010-külső perec, 2008-belső perec) – KSH adatai szerint
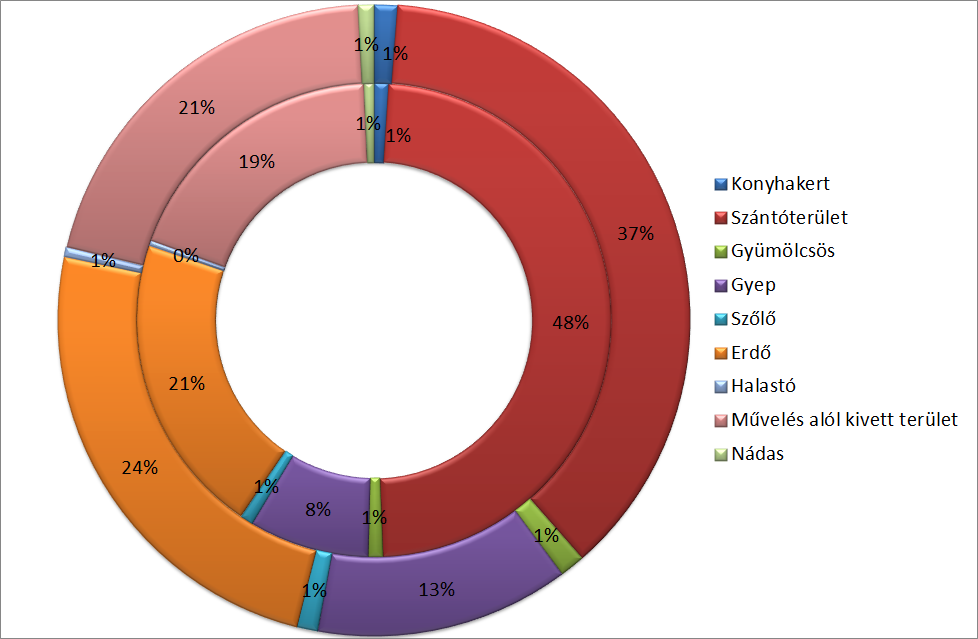 |
Az oszlopdiagramok a nagyságok, eloszlások, vagy részekből összetevődő egész alkotóelemeinek egymáshoz való viszonyát (halmozott oszlop) képesek szemléltetni. Az oszlopok nagysága rendszerint arányos az ábrázolni kívánt mennyiséggel.
Az oszlopdiagram szerkezete alapján lehet egyszerű, kétirányú (két egymással logikailag összefüggő adatsor esetén, 9.7 ábra), osztott (összetétel ábrázolása, 9.8 ábra). Speciális változata a gyakorisági eloszlások szemléltetésére használt ún. hisztogram, melynek vízszintes tengelyén az osztályokat, függőleges tengelyén a gyakoriságokat ábrázoljuk (9.7 ábra).
Tartalom
Bármilyen adatfeldolgozás első lépése az adatsor ellenőrzése, melynek során a kiugró, nem reális értékeket ki kell zárni az értékelésből. Számolnunk kell azzal a ténnyel is, hogy hosszú időtartamú mérések esetén meghibásodás, kalibrálás miatt mindig történik adatkiesés is. A hatályos jogszabály alapján ahhoz, hogy az értékelés elfogadható legyen, minimálisan 90 %-os adatmennyiség szükséges.
Az adatok magas szintű kezelésének az alapja a kapcsolati vizsgálatok. A kapcsolati vizsgálatok környezetvédelemben használt leggyakoribb típusa a koncentráció görbe és a Lorenz.
A összes adat jelentős részének kis tartományba történő csoportosulását koncentrációnak nevezzük.
Típusai:
-
Abszolút (a csoportosulás nagyon kis tartományba történik)
-
Relatív (a teljes tartományhoz képest kicsi a tömörülés)
-
Negatív (ha egyenletes az eloszlás)
A koncentráció ábrázolását Lorenz görbével szoktuk megoldani. Ezt rangsorból vagy osztályközös kumulált relatív gyakoriságból állítjuk elő.
A Lorencz görbe egy egységoldalú (jellemzően 100*100-as) négyzetben elhelyezett ábra, ami a kumulált relatív gyakoriságok függvényében ábrázolja a kumulált relatív értékösszegeket. Amennyiben az egységeknek az értékösszegből való részesedése azonos, azaz teljesen egyenletes az eloszlás, akkor a kumulált relatív gyakoriságok és a kumulált relatív értékösszegek minden esetbe megegyeznek. Ekkor a görbe azonos a négyzet átlójával. (Teljes egyenlőség áll fenn.)
Előfordulhat, hogy teljes koncentráció, vagyis teljes egyenlőtlenség lép fel, ebben az esetben a görbe egybeesik a négyzet oldalaival (azaz a tengelyekkel).
A Lorenz görbe kiemelt jelentőségű része a koncentrációs terület, azaz az átló és a Lorenz görbe által bezárt terület. Minél nagyobb ez a terület, annál nagyobb a koncentráció. Bizonyos esetekben a görbe már nem ad értékelhető eredményt, ezért azt számszerűsíteni kell. Erre szolgál a Gini együttható.
Számítása:
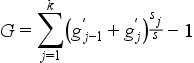
Példa:
Egy ipari parkban 14 szennyvíz-forrás üzemel. Ábrázoljuk, illetve fejezzük ki Gini együtthatóval, mennyire egyenletesen veszik ki a részüket az ipari park összes szennyezéséből az egyes források.
11.1. táblázat - Szennyvízkibocsátók az ipari parkban.
|
A |
B |
C |
D | |
|---|---|---|---|---|
|
1 |
Forrás megnevezése |
Szennyvíz kibocsájtás (m3/nap) |
→ |
Rangsor |
|
2 |
Kis ZRt. |
100 |
50 | |
|
3 |
Lakatos Kft. |
250 |
90 | |
|
4 |
Kereki Kft. |
110 |
100 | |
|
5 |
Kovács ZRt. |
340 |
100 | |
|
6 |
Szalonka NyRt. |
50 |
110 | |
|
7 |
Kocsis Kft. |
230 |
110 | |
|
8 |
Nyulas Kft. |
170 |
120 | |
|
9 |
Tamás NyRt. |
210 |
150 | |
|
10 |
Mérleg ZRt. |
100 |
170 | |
|
11 |
Takács Kft. |
120 |
210 | |
|
12 |
Motoros Kft. |
90 |
230 | |
|
13 |
Keleti ZRt. |
150 |
230 | |
|
14 |
Lajos Kft. |
110 |
250 | |
|
15 |
Kertész Kft. |
230 |
340 |
Első lépésként rangsort (lásd. fent), majd osztályközös gyakoriságokat készítünk.
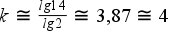
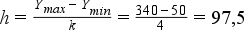
A fenti egyenleteket MS Office és LiberOffice esetén a következő módon tudjuk kiszámolni:
11.2. táblázat - Előzetes számítások a Gini-együtthatóhoz.
|
F |
G | |
|---|---|---|
|
1 |
Osztályközös gyakoriság | |
|
2 |
N |
14* |
|
3 |
k |
4** |
|
4 |
h |
97,5*** |
* MS Office esetén: =DARAB(D:D)
* LibreOffice esetén: =DARAB(D2:D15)
** MS Office esetén: =KEREK.FEL(LOG10(DARAB(D:D))/LOG10(2);0)
** LibreOffice esetén: =KEREK.FEL(LOG(DARAB(D2:D15);10)/LOG(2;10);0)
***MS Office és LibreOffice esetén: =(MAX(D:D)- MIN(D:D))/G3
Következő lépésben létrehozzuk az osztályközöket:
11.3. táblázat - Osztályközök létrehozása.
|
J |
K |
L |
M | |
|---|---|---|---|---|
|
1 |
Yi0 |
Yi1 |
Xi |
fi |
|
2 |
50 |
122 |
86 |
7 |
|
3 |
123 |
195 |
159 |
2 |
|
4 |
196 |
267 |
231,5 |
4 |
|
5 |
268 |
340 |
304 |
1 |
Ehhez a táblázathoz az alábbi makrót kellet használni MS Office-ban:
Sub Ösztályköz_képzés()
Dim Köz As Double
Dim t, r As Integer
Köz = Cells(2, 4)
For t = 1 To Cells(3, 7)
If t = 1 Then
Cells(t + 1, 10) = Int(Köz)
Else
Cells(t + 1, 10) = Cells(t, 11) + 1
End If
Köz = Köz + Cells(4, 7)
Cells(t + 1, 11) = Int(Köz)
Cells(t + 1, 12) = (Cells(t + 1, 10) + Cells(t + 1, 11))/2
Next t
r = 0
Köz = 1
For t = 2 To Cells(2, 7) + 1
If Cells(Köz + 1, 11) >= Cells(t, 4) Then
'Még az aktuális osztályközben vagyunk
r = r + 1
Else
’Új közbe léptünk
Cells(Köz + 1, 13) = r
Köz = Köz + 1
r = 1
End If
Next t
End Sub
Következő lépésként a relatív gyakoriságot és a relatív kumulált gyakoriságot számoljuk ki:
11.4. táblázat - Gyakoriságok értékei.
|
M |
N |
O | |
|---|---|---|---|
|
1 |
fi |
gi |
g’i |
|
2 |
7 |
0,500 |
0,500 |
|
3 |
2 |
0,143 |
0,643 |
|
4 |
4 |
0,286 |
0,929 |
|
5 |
1 |
0,071 |
1,000 |
Ezt MS Office és LiberOffice esetén is a következő képletekkel értük el:
11.5. táblázat - Gyakoriságok számítása.
|
M |
N |
O | |
|---|---|---|---|
|
1 |
fi |
gi |
g’i |
|
2 |
7 |
=M2/$G$2 |
=N2 |
|
3 |
2 |
=M3/$G$2 |
=O2+N3 |
|
4 |
4 |
=M4/$G$2 |
=O3+N4 |
|
5 |
1 |
=M5/$G$2 |
=O4+N5 |
Ezután meghatározzuk a relatív értékösszegsort és a kumulált relatív értékösszegsort:
11.6. táblázat - Érkékösszegsorok.
|
P |
R |
O | |
|---|---|---|---|
|
1 |
si |
Zii |
s’i |
|
2 |
602 |
0,280 |
0,280 |
|
3 |
318 |
0,148 |
0,428 |
|
4 |
926 |
0,431 |
0,859 |
|
5 |
304 |
0,141 |
1,000 |
Ezt MS Office és LiberOffice esetén is a következő képletekkel értük el:
11.7. táblázat - Értékösszegsorok számítási módja.
|
P |
Q |
R | |
|---|---|---|---|
|
1 |
si |
Zii |
s’i |
|
2 |
=L2*M2 |
=P2/SZUM(P2:P5) |
=Q2 |
|
3 |
=L3*M3 |
=P3/SZUM(P2:P5) |
=Q3+R2 |
|
4 |
=L4*M4 |
=P4/SZUM(P2:P5) |
=Q4+R3 |
|
5 |
=L5*M5 |
=P5/SZUM(P2:P5) |
=Q5+R4 |
A Lorenz görbe megrajzolásához a relatív kumulált gyakoriságot (O oszlop) kell ábrázolni a kumulált relatív értékösszegsor függvényében. (Javasolt XY grafikont alkalmazni.) Az eredmény a következő lesz:
A Gini együttható meghatározásához érdemes segédtáblázatot készíteni:
11.8. táblázat - Gini együtthatóhoz szükséges segédtábla
|
S |
T |
U |
V | |
|---|---|---|---|---|
|
1 |
|
| ||
|
2 |
0,140 |
0,000 | ||
|
3 |
0,095 |
0,074 |
Gini együttható: | |
|
4 |
0,400 |
0,277 |
0,259 | |
|
5 |
0,141 |
0,131 | ||
|
6 |
Összesen: |
0,776 |
0,482 |
Ezt MS Office és LiberOffice esetén is a következő képletekkel értük el:
11.9. táblázat - Gini együtthatóhoz szükséges segédszámítások.
|
S |
T |
U |
V | |
|---|---|---|---|---|
|
1 |
|
| ||
|
2 |
=O2*P2/SZUM($P$2:$P$5) |
0 | ||
|
3 |
=O3*P3/SZUM($P$2:$P$5) |
=O2*P3/SZUM($P$2:$P$5) |
Gini együttható: | |
|
4 |
=O4*P4/SZUM($P$2:$P$5) |
=O3*P4/SZUM($P$2:$P$5) |
=T6+U6-1 | |
|
5 |
=O5*P5/SZUM($P$2:$P$5) |
=O4*P5/SZUM($P$2:$P$5) | ||
|
6 |
Összesen: |
=SZUM(T2:T5) |
=SZUM(U2:U5) |
A Gini együttható értéke 0,259 (igen kis mértékű koncentráció tapasztalható), ami azt jelenti, hogy a szennyezők közül bár vannak nagyobbak, egyikük sem erőteljes annyira, hogy a szennyvízkibocsátása meghatározó legyen.
Tartalom
Az emberi élet minőségét jelentősen befolyásolja a környezeti levegő minőségének alakulása. Egy lakott terület levegőminőségét elsősorban a lakosság életvitele, a hatásterületen belüli ipari tevékenység és a közlekedésből származó levegőszennyezés határozza meg.
Jelen fejezetben a „Székesfehérvár - Veszprém Pólustengely” közepén fekvő Várpalota város példáján keresztül vizsgáljuk meg diagramok segítségével a levegőminőség változását, a főbb levegőszennyező forrásokat, és a komponensenkénti megoszlást a több évtizedes trend alapján. Az adatsorok az OLM rendszeréből, továbbá a KDT-KTVF Veszprémi Levegőtisztaság-védelmi Laboratóriumából származnak.
Várpalota a Dunántúlon, Veszprém megye északkeleti szélén terül el. A lakosság számát tekintve a megye negyedik legnagyobb városa. Budapesttől 90 km-e, két megyeszékhely, Székesfehérvár és Veszprém között félúton fekszik, a Bakony lábánál, a Balatontól alig 30 km-re.
Várpalota[7] város fejlettségét az elmúlt fél évszázadban döntően a nehéziparral lehetne jellemezni. Így érthető, hogy a térség környezeti és levegőminőségi állapota az országos átlagnál lényegesen rosszabb volt. Fontos azonban megjegyeznünk, hogy az ipari szennyezések – melyek elsődlegesen a várpalotai szénbányászathoz, Inotai Hőerőműhöz, Alumíniumkohóhoz, Nitrogénművek Zrt.-hez voltak köthetők – jelentősen csökkentek az elmúlt években, amely elsősorban a 90-es évek változásainak köszönhető:
-
a nehézipar összeomlása,
-
1996-ban véglegesen megszűnt a szénbányászat, a Földtani Kutató és Fúró Kft,
-
1997-ben felszámolták az addig stabilnak hitt Vegyesipari Szövetkezet is.
A 90-es évek második felében a város és térsége jelentős fejlesztéseket valósított meg, amely főként az 1995-ben elnyert japán hitelből jöhetett létre. A fejlesztéseket az a tény is nélkülözhetetlenné tette, hogy egy rendszerváltás előtti felmérés az ország egyik legszennyezettebb területének minősítette Várpalotát és térségét. Megvalósult többek között Várpalota és további öt település – Berhida, Ősi, Öskü, Pétfürdő, Tés - földgáz- és ivóvízellátását, valamint a szennyvíztisztítás fejlesztését célzó program is, amely 1995 szeptemberében kezdődött és 1998. október végéig el is készült.
A következőkben nézzük meg a legjelentősebb légszennyező anyagok koncentrációinak változását, miként változtak az évtizedek során.
12.1. ábra - Várpalota, Inota, Pétfürdő – NO2 koncentrációk éves átlagértékeinek változása 1979-2008 között
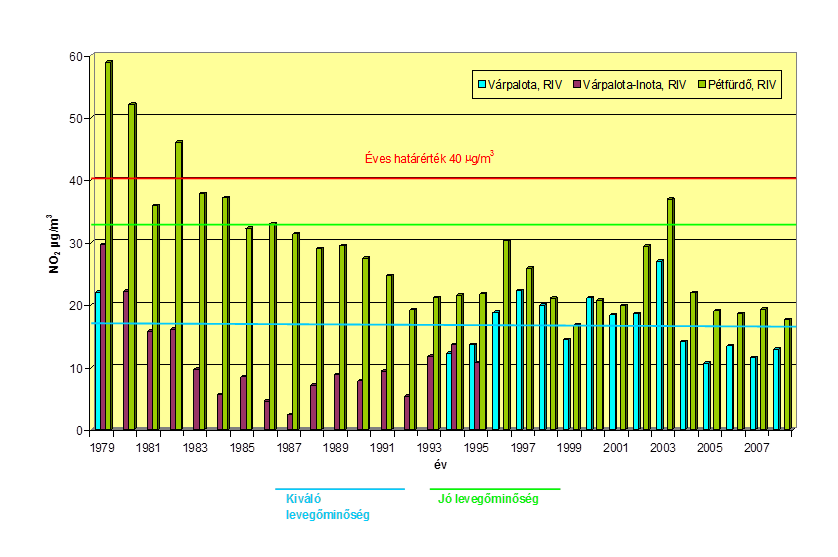 |
12.2. ábra - Várpalota, Pétfürdő – SO2 koncentrációk éves átlagértékeinek változása 1979-2008 között
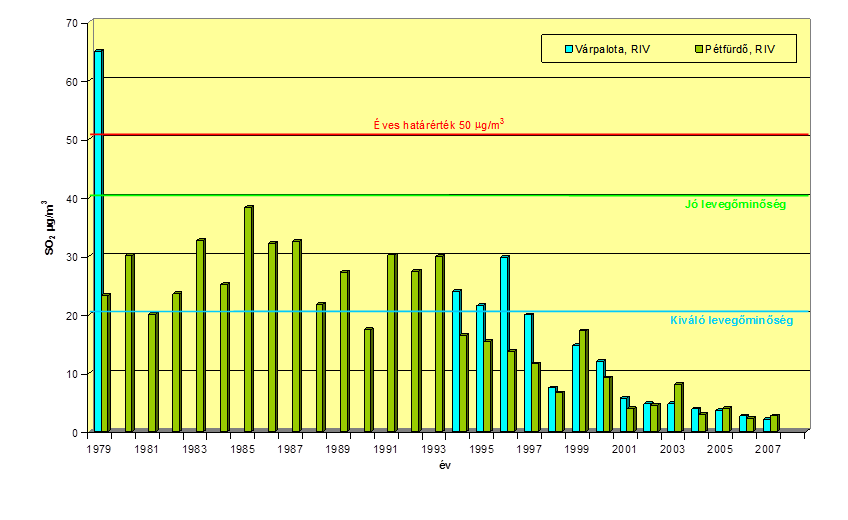 |
A 11.1 - 11.4. számú diagramokon jól látható, hogy a régebben jelentős mértékben szennyezett levegőjű Várpalota és környéke jelentős változáson ment keresztül és megy napjainkban is. Várpalota esetében elmondható – csakúgy, mint városaink nagy többségénél –, hogy ma már leginkább a közlekedésből származó emisszió okoz esetenként magasabb szennyezőanyag-koncentrációt.
Különösen a nitrogén-oxidok és a szálló por légköri koncentrációjának alakulását kell figyelemmel kísérnünk, tekintettel arra, hogy a kedvezőtlen meteorológiai körülmények között ezen anyagok koncentrációja esetleg meghaladhatja a határértéket, továbbá nyári hónapokban az ózon koncentrációja lehet átmenetileg magasabb a megengedett egészségügyi határértékeknél. Összességében azonban elmondható, hogy Várpalota ma már a közepes légszennyezettségű városok közé tartozik.
Pétfürdőn szintén nagymértékű javulás tapasztalható, csakúgy, mint Várpalota-Inotán. Amíg a levegőszennyezettség csökkenése Pétfürdőn főként a Nitrogénművek Zrt. kibocsátásainak mérséklődése, valamint a technológia korszerűsödése folytán következett be, addig Inotán a javulás legfőbb oka a hőerőmű, illetve az alumíniumkohó elektrolízis üzemeinek bezárása volt.
A fentebb leírtakat alapul véve a jövőre nézve tehát a vizsgált térségben elsősorban a közlekedési eredetű szennyezőanyagok elleni védekezés jelentheti a fő problémakört (ugyanis a 8. számú főút forgalma jelentősen terheli Várpalota és Inota települését is).
Nehéz megfogalmazni mi is lehetne az a megoldás, amit mindenki a sajátjának érezhetne, és be is betartana. A levegőszennyezettség kialakulásának megakadályozására – főként a nitrogén-oxidok és a szálló por koncentrációja tekintetében – alkalmas intézkedés lehetne például a lámpás kereszteződések körforgalmi csomópontokra történő átépítése is, melynek következtében az átmenő forgalom a városon keresztül történő folyamatos, megállás nélküli áthaladással kevésbé terheli a levegőt. Hatékony megoldás lehetne továbbá Várpalotán a zöldterületek növelése, valamint a 8-as út menti fásítás, amely intézkedések szintén nagyban hozzájárulnának a város levegőjének javulásához.
ELLENŐRZŐ KÉRDÉSEK
Mutassa be az adatbázisok alkalmazásának jogi hátterét!
Milyen módszereket ismer az adatok kiértékelésére?
Ismertesse Várpalota levegőminőségének változását az elmúlt 30 év távlatában!
[7] A „piszkos tizenkettő” névvel illetett városok közé tartozott. Így nevezték el a legszennyezettebb levegőjű városokat Magyarországon.
Dr. Szabó Imre (szerk.): Környezetinformatika Pannon Egyetem 2008. (elektronikus jegyzet http://mkweb.uni-pannon.hu/hefop33//anyagok.html)
Vág András: Statisztika online - oktatási portál Typotex, 2005 http://www.tankonyvtar.hu/konyvek/statisztika-online/statisztika-online-090211-11
Fidy Judit , Makara Gábor dr.: Biostatisztika Typotex, 2005 http://www.tankonyvtar.hu/statisztika/biostatisztika-080904-92
Michelberger Pál – Szeidl László – Várlaki Péter: Alkalmazott folyamatstatisztika és idősor-analízis, Alkalmazott matematika sorozat Typotex Kiadó, 2001
Borovkov, A. A: Matematikai statisztika Typotex Elektronikus Kiadó, 1999
Kröpfl-Peschek-Schneider-Schönlieb: Alkalmazott statisztika Műszaki Könyvkiadó, 2000
Szűcs István (szerk.): Alkalmazott statisztika Agroinform Kiadóház, 2004
Dr. Abonyi János (szerk.): Adatbányászat - a hatékonyság eszköze, Computerbooks 2006.
Dr. Bodon Ferenc: Adatbányászati algoritmusok, Budapesti Műszaki és Gazdaságtudományi Egyetem, 2010 (elektronikus jegyzet) http://www.cs.bme.hu/~bodon/magyar/adatbanyaszat/tanulmany/adatbanyaszat.pdf
Dr. Harnos Zsolt, Dr. Herdon Miklós (szerk): Informatikai alapok, Debreceni Egyetem Agrártudományi Centrum, Agrárgazdasági és Vidékfejlesztési Kar, 2006 (elektronikus jegyzet)
1. Segédtáblázat: χ2 eloszlás kritikus értékei (χ2 próbához) 0,999-0,50 tartományban
|
DF\χ2 |
0,999 |
0,99 |
0,98 |
0,95 |
0,90 |
0,80 |
0,50 |
|---|---|---|---|---|---|---|---|
|
1 |
0,0000 |
0,0002 |
0,0006 |
0,0039 |
0,0158 |
0,0642 |
0,4549 |
|
2 |
0,0020 |
0,0201 |
0,0404 |
0,1026 |
0,2107 |
0,4463 |
1,3863 |
|
3 |
0,0243 |
0,1148 |
0,1848 |
0,3518 |
0,5844 |
1,0052 |
2,3660 |
|
4 |
0,0908 |
0,2971 |
0,4294 |
0,7107 |
1,0636 |
1,6488 |
3,3567 |
|
5 |
0,2102 |
0,5543 |
0,7519 |
1,1455 |
1,6103 |
2,3425 |
4,3515 |
|
6 |
0,3811 |
0,8721 |
1,1344 |
1,6354 |
2,2041 |
3,0701 |
5,3481 |
|
7 |
0,5985 |
1,2390 |
1,5643 |
2,1673 |
2,8331 |
3,8223 |
6,3458 |
|
8 |
0,8571 |
1,6465 |
2,0325 |
2,7326 |
3,4895 |
4,5936 |
7,3441 |
|
9 |
1,1519 |
2,0879 |
2,5324 |
3,3251 |
4,1682 |
5,3801 |
8,3428 |
|
10 |
1,4787 |
2,5582 |
3,0591 |
3,9403 |
4,8652 |
6,1791 |
9,3418 |
|
11 |
1,8339 |
3,0535 |
3,6087 |
4,5748 |
5,5778 |
6,9887 |
10,3410 |
|
12 |
2,2142 |
3,5706 |
4,1783 |
5,2260 |
6,3038 |
7,8073 |
11,3403 |
|
13 |
2,6172 |
4,1069 |
4,7654 |
5,8919 |
7,0415 |
8,6339 |
12,3398 |
|
14 |
3,0407 |
4,6604 |
5,3682 |
6,5706 |
7,7895 |
9,4673 |
13,3393 |
|
15 |
3,4827 |
5,2293 |
5,9849 |
7,2609 |
8,5468 |
10,3070 |
14,3389 |
|
16 |
3,9416 |
5,8122 |
6,6142 |
7,9616 |
9,3122 |
11,1521 |
15,3385 |
|
17 |
4,4161 |
6,4078 |
7,2550 |
8,6718 |
10,0852 |
12,0023 |
16,3382 |
|
18 |
4,9048 |
7,0149 |
7,9062 |
9,3905 |
10,8649 |
12,8570 |
17,3379 |
|
19 |
5,4068 |
7,6327 |
8,5670 |
10,1170 |
11,6509 |
13,7158 |
18,3377 |
|
20 |
5,9210 |
8,2604 |
9,2367 |
10,8508 |
12,4426 |
14,5784 |
19,3374 |
|
21 |
6,4467 |
8,8972 |
9,9146 |
11,5913 |
13,2396 |
15,4446 |
20,3372 |
|
22 |
6,9830 |
9,5425 |
10,6000 |
12,3380 |
14,0415 |
16,3140 |
21,3370 |
|
23 |
7,5292 |
10,1957 |
11,2926 |
13,0905 |
14,8480 |
17,1865 |
22,3369 |
|
24 |
8,0849 |
10,8564 |
11,9918 |
13,8484 |
15,6587 |
18,0618 |
23,3367 |
|
25 |
8,6493 |
11,5240 |
12,6973 |
14,6114 |
16,4734 |
18,9398 |
24,3366 |
|
26 |
9,2221 |
12,1981 |
13,4086 |
15,3792 |
17,2919 |
19,8202 |
25,3365 |
|
27 |
9,8028 |
12,8785 |
14,1254 |
16,1514 |
18,1139 |
20,7030 |
26,3363 |
|
28 |
10,3909 |
13,5647 |
14,8475 |
16,9279 |
18,9392 |
21,5880 |
27,3362 |
|
29 |
10,9861 |
14,2565 |
15,5745 |
17,7084 |
19,7677 |
22,4751 |
28,3361 |
|
30 |
11,5880 |
14,9535 |
16,3062 |
18,4927 |
20,5992 |
23,3641 |
29,3360 |
|
31 |
12,1963 |
15,6555 |
17,0423 |
19,2806 |
21,4336 |
24,2551 |
30,3359 |
|
32 |
12,8107 |
16,3622 |
17,7827 |
20,0719 |
22,2706 |
25,1478 |
31,3359 |
|
33 |
13,4309 |
17,0735 |
18,5271 |
20,8665 |
23,1102 |
26,0422 |
32,3358 |
|
34 |
14,0567 |
17,7891 |
19,2754 |
21,6643 |
23,9523 |
26,9383 |
33,3357 |
|
35 |
14,6878 |
18,5089 |
20,0274 |
22,4650 |
24,7967 |
27,8359 |
34,3356 |
|
36 |
15,3241 |
19,2327 |
20,7829 |
23,2686 |
25,6433 |
28,7350 |
35,3356 |
|
37 |
15,9653 |
19,9602 |
21,5419 |
24,0749 |
26,4921 |
29,6355 |
36,3355 |
|
38 |
16,6112 |
20,6914 |
22,3040 |
24,8839 |
27,3430 |
30,5373 |
37,3355 |
|
39 |
17,2616 |
21,4262 |
23,0693 |
25,6954 |
28,1958 |
31,4405 |
38,3354 |
|
40 |
17,9164 |
22,1643 |
23,8376 |
26,5093 |
29,0505 |
32,3450 |
39,3353 |
|
41 |
18,5754 |
22,9056 |
24,6087 |
27,3256 |
29,9071 |
33,2506 |
40,3353 |
|
42 |
19,2385 |
23,6501 |
25,3827 |
28,1440 |
30,7654 |
34,1574 |
41,3352 |
|
43 |
19,9055 |
24,3976 |
26,1594 |
28,9647 |
31,6255 |
35,0653 |
42,3352 |
|
44 |
20,5763 |
25,1480 |
26,9386 |
29,7875 |
32,4871 |
35,9743 |
43,3352 |
|
45 |
21,2507 |
25,9013 |
27,7203 |
30,6123 |
33,3504 |
36,8844 |
44,3351 |
|
46 |
21,9287 |
26,6572 |
28,5045 |
31,4390 |
34,2152 |
37,7955 |
45,3351 |
|
47 |
22,6101 |
27,4158 |
29,2910 |
32,2676 |
35,0814 |
38,7075 |
46,3350 |
|
48 |
23,2949 |
28,1770 |
30,0798 |
33,0981 |
35,9491 |
39,6205 |
47,3350 |
|
49 |
23,9828 |
28,9406 |
30,8708 |
33,9303 |
36,8182 |
40,5344 |
48,3350 |
|
50 |
24,6739 |
29,7067 |
31,6639 |
34,7643 |
37,6886 |
41,4492 |
49,3349 |
|
51 |
25,3680 |
30,4750 |
32,4590 |
35,5999 |
38,5604 |
42,3649 |
50,3349 |
|
52 |
26,0651 |
31,2457 |
33,2562 |
36,4371 |
39,4334 |
43,2814 |
51,3349 |
|
53 |
26,7650 |
32,0185 |
34,0553 |
37,2759 |
40,3076 |
44,1987 |
52,3348 |
|
54 |
27,4677 |
32,7934 |
34,8563 |
38,1162 |
41,1830 |
45,1167 |
53,3348 |
|
55 |
28,1731 |
33,5705 |
35,6592 |
38,9580 |
42,0596 |
46,0356 |
54,3348 |
|
56 |
28,8812 |
34,3495 |
36,4639 |
39,8013 |
42,9373 |
46,9552 |
55,3348 |
|
57 |
29,5918 |
35,1305 |
37,2702 |
40,6459 |
43,8161 |
47,8755 |
56,3347 |
|
58 |
30,3049 |
35,9135 |
38,0783 |
41,4920 |
44,6960 |
48,7965 |
57,3347 |
|
59 |
31,0204 |
36,6982 |
38,8881 |
42,3393 |
45,5770 |
49,7182 |
58,3347 |
|
60 |
31,7383 |
37,4849 |
39,6994 |
43,1880 |
46,4589 |
50,6406 |
59,3347 |
|
61 |
32,4586 |
38,2732 |
40,5123 |
44,0379 |
47,3418 |
51,5636 |
60,3346 |
|
62 |
33,1811 |
39,0633 |
41,3268 |
44,8890 |
48,2257 |
52,4873 |
61,3346 |
|
63 |
33,9058 |
39,8551 |
42,1428 |
45,7414 |
49,1105 |
53,4116 |
62,3346 |
|
64 |
34,6326 |
40,6486 |
42,9602 |
46,5949 |
49,9963 |
54,3365 |
63,3346 |
|
65 |
35,3616 |
41,4436 |
43,7790 |
47,4496 |
50,8829 |
55,2620 |
64,3346 |
|
66 |
36,0926 |
42,2402 |
44,5992 |
48,3054 |
51,7705 |
56,1880 |
65,3345 |
|
67 |
36,8257 |
43,0384 |
45,4208 |
49,1623 |
52,6588 |
57,1147 |
66,3345 |
|
68 |
37,5606 |
43,8380 |
46,2437 |
50,0202 |
53,5481 |
58,0418 |
67,3345 |
|
69 |
38,2976 |
44,6392 |
47,0680 |
50,8792 |
54,4381 |
58,9696 |
68,3345 |
|
70 |
39,0364 |
45,4417 |
47,8934 |
51,7393 |
55,3289 |
59,8978 |
69,3345 |
|
71 |
39,7770 |
46,2457 |
48,7202 |
52,6003 |
56,2206 |
60,8266 |
70,3345 |
|
72 |
40,5195 |
47,0510 |
49,5481 |
53,4623 |
57,1129 |
61,7558 |
71,3344 |
|
73 |
41,2637 |
47,8577 |
50,3773 |
54,3253 |
58,0061 |
62,6856 |
72,3344 |
|
74 |
42,0097 |
48,6657 |
51,2076 |
55,1892 |
58,9000 |
63,6158 |
73,3344 |
|
75 |
42,7573 |
49,4750 |
52,0391 |
56,0541 |
59,7946 |
64,5466 |
74,3344 |
|
76 |
43,5066 |
50,2856 |
52,8717 |
56,9198 |
60,6899 |
65,4777 |
75,3344 |
|
77 |
44,2576 |
51,0974 |
53,7054 |
57,7864 |
61,5858 |
66,4094 |
76,3344 |
|
78 |
45,0101 |
51,9104 |
54,5401 |
58,6539 |
62,4825 |
67,3415 |
77,3344 |
|
79 |
45,7642 |
52,7247 |
55,3760 |
59,5223 |
63,3799 |
68,2740 |
78,3343 |
|
80 |
46,5199 |
53,5401 |
56,2128 |
60,3915 |
64,2778 |
69,2069 |
79,3343 |
|
81 |
47,2770 |
54,3566 |
57,0507 |
61,2615 |
65,1765 |
70,1403 |
80,3343 |
|
82 |
48,0357 |
55,1743 |
57,8896 |
62,1323 |
66,0757 |
71,0741 |
81,3343 |
|
83 |
48,7958 |
55,9931 |
58,7295 |
63,0039 |
66,9756 |
72,0083 |
82,3343 |
|
84 |
49,5573 |
56,8130 |
59,5703 |
63,8763 |
67,8761 |
72,9429 |
83,3343 |
|
85 |
50,3203 |
57,6339 |
60,4121 |
64,7494 |
68,7772 |
73,8779 |
84,3343 |
|
86 |
51,0846 |
58,4559 |
61,2548 |
65,6233 |
69,6788 |
74,8132 |
85,3343 |
|
87 |
51,8503 |
59,2790 |
62,0984 |
66,4979 |
70,5810 |
75,7490 |
86,3342 |
|
88 |
52,6173 |
60,1030 |
62,9430 |
67,3732 |
71,4838 |
76,6851 |
87,3342 |
|
89 |
53,3856 |
60,9281 |
63,7884 |
68,2493 |
72,3872 |
77,6216 |
88,3342 |
|
90 |
54,1552 |
61,7541 |
64,6347 |
69,1260 |
73,2911 |
78,5584 |
89,3342 |
|
91 |
54,9261 |
62,5811 |
65,4818 |
70,0035 |
74,1955 |
79,4956 |
90,3342 |
|
92 |
55,6983 |
63,4090 |
66,3298 |
70,8816 |
75,1005 |
80,4332 |
91,3342 |
|
93 |
56,4716 |
64,2379 |
67,1786 |
71,7603 |
76,0060 |
81,3711 |
92,3342 |
|
94 |
57,2462 |
65,0677 |
68,0282 |
72,6398 |
76,9119 |
82,3093 |
93,3342 |
|
95 |
58,0220 |
65,8984 |
68,8786 |
73,5198 |
77,8184 |
83,2478 |
94,3342 |
|
96 |
58,7989 |
66,7299 |
69,7298 |
74,4005 |
78,7254 |
84,1867 |
95,3342 |
|
97 |
59,5770 |
67,5624 |
70,5817 |
75,2819 |
79,6329 |
85,1259 |
96,3342 |
|
98 |
60,3562 |
68,3957 |
71,4345 |
76,1638 |
80,5408 |
86,0654 |
97,3341 |
|
99 |
61,1365 |
69,2299 |
72,2880 |
77,0463 |
81,4493 |
87,0052 |
98,3341 |
|
100 |
61,9179 |
70,0649 |
73,1422 |
77,9295 |
82,3581 |
87,9453 |
99,3341 |
|
110 |
69,7894 |
78,4583 |
81,7228 |
86,7916 |
91,4710 |
97,3624 |
109,3341 |
|
120 |
77,7551 |
86,9233 |
90,3667 |
95,7046 |
100,6236 |
106,8056 |
119,3340 |
|
130 |
85,8037 |
95,4510 |
99,0662 |
104,6622 |
109,8110 |
116,2717 |
129,3339 |
|
140 |
93,9256 |
104,0344 |
107,8149 |
113,6593 |
119,0293 |
125,7581 |
139,3339 |
|
150 |
102,1133 |
112,6676 |
116,6076 |
122,6918 |
128,2751 |
135,2625 |
149,3339 |
|
160 |
110,3603 |
121,3456 |
125,4400 |
131,7561 |
137,5457 |
144,7834 |
159,3338 |
|
170 |
118,6611 |
130,0644 |
134,3084 |
140,8492 |
146,8389 |
154,3190 |
169,3338 |
|
180 |
127,0111 |
138,8204 |
143,2096 |
149,9688 |
156,1526 |
163,8682 |
179,3338 |
|
190 |
135,4061 |
147,6104 |
152,1411 |
159,1125 |
165,4853 |
173,4298 |
189,3338 |
|
200 |
143,8428 |
156,4320 |
161,1003 |
168,2786 |
174,8353 |
183,0028 |
199,3337 |
|
210 |
152,3180 |
165,2826 |
170,0852 |
177,4652 |
184,2014 |
192,5864 |
209,3337 |
|
220 |
160,8290 |
174,1604 |
179,0941 |
186,6711 |
193,5825 |
202,1798 |
219,3337 |
|
230 |
169,3734 |
183,0633 |
188,1253 |
195,8949 |
202,9775 |
211,7824 |
229,3337 |
|
240 |
177,9491 |
191,9899 |
197,1774 |
205,1354 |
212,3856 |
221,3936 |
239,3337 |
|
250 |
186,5541 |
200,9386 |
206,2490 |
214,3916 |
221,8059 |
231,0128 |
249,3337 |
|
260 |
195,1867 |
209,9082 |
215,3391 |
223,6625 |
231,2378 |
240,6396 |
259,3336 |
|
270 |
203,8453 |
218,8974 |
224,4465 |
232,9474 |
240,6804 |
250,2735 |
269,3336 |
|
280 |
212,5285 |
227,9051 |
233,5703 |
242,2454 |
250,1334 |
259,9142 |
279,3336 |
|
290 |
221,2349 |
236,9305 |
242,7096 |
251,5559 |
259,5960 |
269,5612 |
289,3336 |
|
300 |
229,9634 |
245,9725 |
251,8637 |
260,8781 |
269,0679 |
279,2143 |
299,3336 |
|
350 |
273,9020 |
291,4058 |
297,8312 |
307,6476 |
316,5504 |
327,5607 |
349,3336 |
|
400 |
318,2596 |
337,1553 |
344,0781 |
354,6410 |
364,2074 |
376,0218 |
399,3335 |
|
450 |
362,9598 |
383,1633 |
390,5532 |
401,8173 |
412,0071 |
424,5766 |
449,3335 |
|
500 |
407,9470 |
429,3875 |
437,2194 |
449,1468 |
459,9261 |
473,2099 |
499,3335 |
|
550 |
453,1789 |
475,7964 |
484,0486 |
496,6068 |
507,9470 |
521,9100 |
549,3335 |
|
600 |
498,6229 |
522,3651 |
531,0191 |
544,1801 |
556,0560 |
570,6680 |
599,3335 |
|
650 |
544,2530 |
569,0741 |
578,1134 |
591,8526 |
604,2424 |
619,4769 |
649,3335 |
|
700 |
590,0480 |
615,9075 |
625,3175 |
639,6130 |
652,4973 |
668,3308 |
699,3334 |
|
750 |
635,9907 |
662,8521 |
672,6198 |
687,4522 |
700,8136 |
717,2250 |
749,3334 |
|
800 |
682,0665 |
709,8969 |
720,0107 |
735,3623 |
749,1852 |
766,1555 |
799,3334 |
|
850 |
728,2630 |
757,0328 |
767,4820 |
783,3369 |
797,6070 |
815,1189 |
849,3334 |
|
900 |
774,5698 |
804,2517 |
815,0267 |
831,3702 |
846,0746 |
864,1125 |
899,3334 |
|
950 |
820,9778 |
851,5469 |
862,6386 |
879,4574 |
894,5842 |
913,1337 |
949,3334 |
|
1000 |
867,4791 |
898,9124 |
910,3127 |
927,5944 |
943,1326 |
962,1803 |
999,3334 |
2. Segédtáblázat: χ2eloszlás kritikus értékei (χ2 próbához) 0,20-0,001 tartományban
|
DF\χ2 |
0,20 |
0,10 |
0,05 |
0,02 |
0,01 |
0,001 |
|---|---|---|---|---|---|---|
|
1 |
1,6424 |
2,7055 |
3,8415 |
5,4119 |
6,6349 |
10,8276 |
|
2 |
3,2189 |
4,6052 |
5,9915 |
7,8240 |
9,2103 |
13,8155 |
|
3 |
4,6416 |
6,2514 |
7,8147 |
9,8374 |
11,3449 |
16,2662 |
|
4 |
5,9886 |
7,7794 |
9,4877 |
11,6678 |
13,2767 |
18,4668 |
|
5 |
7,2893 |
9,2364 |
11,0705 |
13,3882 |
15,0863 |
20,5150 |
|
6 |
8,5581 |
10,6446 |
12,5916 |
15,0332 |
16,8119 |
22,4577 |
|
7 |
9,8032 |
12,0170 |
14,0671 |
16,6224 |
18,4753 |
24,3219 |
|
8 |
11,0301 |
13,3616 |
15,5073 |
18,1682 |
20,0902 |
26,1245 |
|
9 |
12,2421 |
14,6837 |
16,9190 |
19,6790 |
21,6660 |
27,8772 |
|
10 |
13,4420 |
15,9872 |
18,3070 |
21,1608 |
23,2093 |
29,5883 |
|
11 |
14,6314 |
17,2750 |
19,6751 |
22,6179 |
24,7250 |
31,2641 |
|
12 |
15,8120 |
18,5493 |
21,0261 |
24,0540 |
26,2170 |
32,9095 |
|
13 |
16,9848 |
19,8119 |
22,3620 |
25,4715 |
27,6882 |
34,5282 |
|
14 |
18,1508 |
21,0641 |
23,6848 |
26,8728 |
29,1412 |
36,1233 |
|
15 |
19,3107 |
22,3071 |
24,9958 |
28,2595 |
30,5779 |
37,6973 |
|
16 |
20,4651 |
23,5418 |
26,2962 |
29,6332 |
31,9999 |
39,2524 |
|
17 |
21,6146 |
24,7690 |
27,5871 |
30,9950 |
33,4087 |
40,7902 |
|
18 |
22,7595 |
25,9894 |
28,8693 |
32,3462 |
34,8053 |
42,3124 |
|
19 |
23,9004 |
27,2036 |
30,1435 |
33,6874 |
36,1909 |
43,8202 |
|
20 |
25,0375 |
28,4120 |
31,4104 |
35,0196 |
37,5662 |
45,3147 |
|
21 |
26,1711 |
29,6151 |
32,6706 |
36,3434 |
38,9322 |
46,7970 |
|
22 |
27,3015 |
30,8133 |
33,9244 |
37,6595 |
40,2894 |
48,2679 |
|
23 |
28,4288 |
32,0069 |
35,1725 |
38,9683 |
41,6384 |
49,7282 |
|
24 |
29,5533 |
33,1962 |
36,4150 |
40,2704 |
42,9798 |
51,1786 |
|
25 |
30,6752 |
34,3816 |
37,6525 |
41,5661 |
44,3141 |
52,6197 |
|
26 |
31,7946 |
35,5632 |
38,8851 |
42,8558 |
45,6417 |
54,0520 |
|
27 |
32,9117 |
36,7412 |
40,1133 |
44,1400 |
46,9629 |
55,4760 |
|
28 |
34,0266 |
37,9159 |
41,3371 |
45,4188 |
48,2782 |
56,8923 |
|
29 |
35,1394 |
39,0875 |
42,5570 |
46,6927 |
49,5879 |
58,3012 |
|
30 |
36,2502 |
40,2560 |
43,7730 |
47,9618 |
50,8922 |
59,7031 |
|
31 |
37,3591 |
41,4217 |
44,9853 |
49,2264 |
52,1914 |
61,0983 |
|
32 |
38,4663 |
42,5847 |
46,1943 |
50,4867 |
53,4858 |
62,4872 |
|
33 |
39,5718 |
43,7452 |
47,3999 |
51,7429 |
54,7755 |
63,8701 |
|
34 |
40,6756 |
44,9032 |
48,6024 |
52,9952 |
56,0609 |
65,2472 |
|
35 |
41,7780 |
46,0588 |
49,8018 |
54,2438 |
57,3421 |
66,6188 |
|
36 |
42,8788 |
47,2122 |
50,9985 |
55,4889 |
58,6192 |
67,9852 |
|
37 |
43,9782 |
48,3634 |
52,1923 |
56,7305 |
59,8925 |
69,3465 |
|
38 |
45,0763 |
49,5126 |
53,3835 |
57,9688 |
61,1621 |
70,7029 |
|
39 |
46,1730 |
50,6598 |
54,5722 |
59,2040 |
62,4281 |
72,0547 |
|
40 |
47,2685 |
51,8051 |
55,7585 |
60,4361 |
63,6907 |
73,4020 |
|
41 |
48,3628 |
52,9485 |
56,9424 |
61,6654 |
64,9501 |
74,7449 |
|
42 |
49,4560 |
54,0902 |
58,1240 |
62,8918 |
66,2062 |
76,0838 |
|
43 |
50,5480 |
55,2302 |
59,3035 |
64,1155 |
67,4593 |
77,4186 |
|
44 |
51,6389 |
56,3685 |
60,4809 |
65,3367 |
68,7095 |
78,7495 |
|
45 |
52,7288 |
57,5053 |
61,6562 |
66,5553 |
69,9568 |
80,0767 |
|
46 |
53,8177 |
58,6405 |
62,8296 |
67,7714 |
71,2014 |
81,4003 |
|
47 |
54,9056 |
59,7743 |
64,0011 |
68,9852 |
72,4433 |
82,7204 |
|
48 |
55,9926 |
60,9066 |
65,1708 |
70,1968 |
73,6826 |
84,0371 |
|
49 |
57,0786 |
62,0375 |
66,3386 |
71,4061 |
74,9195 |
85,3506 |
|
50 |
58,1638 |
63,1671 |
67,5048 |
72,6133 |
76,1539 |
86,6608 |
|
51 |
59,2481 |
64,2954 |
68,6693 |
73,8183 |
77,3860 |
87,9680 |
|
52 |
60,3316 |
65,4224 |
69,8322 |
75,0214 |
78,6158 |
89,2722 |
|
53 |
61,4142 |
66,5482 |
70,9935 |
76,2226 |
79,8433 |
90,5734 |
|
54 |
62,4961 |
67,6728 |
72,1532 |
77,4218 |
81,0688 |
91,8718 |
|
55 |
63,5772 |
68,7962 |
73,3115 |
78,6191 |
82,2921 |
93,1675 |
|
56 |
64,6576 |
69,9185 |
74,4683 |
79,8147 |
83,5134 |
94,4605 |
|
57 |
65,7373 |
71,0397 |
75,6237 |
81,0085 |
84,7328 |
95,7510 |
|
58 |
66,8162 |
72,1598 |
76,7778 |
82,2007 |
85,9502 |
97,0388 |
|
59 |
67,8945 |
73,2789 |
77,9305 |
83,3911 |
87,1657 |
98,3242 |
|
60 |
68,9721 |
74,3970 |
79,0819 |
84,5799 |
88,3794 |
99,6072 |
|
61 |
70,0490 |
75,5141 |
80,2321 |
85,7672 |
89,5913 |
100,8879 |
|
62 |
71,1253 |
76,6302 |
81,3810 |
86,9529 |
90,8015 |
102,1662 |
|
63 |
72,2010 |
77,7454 |
82,5287 |
88,1372 |
92,0100 |
103,4424 |
|
64 |
73,2761 |
78,8596 |
83,6753 |
89,3199 |
93,2169 |
104,7163 |
|
65 |
74,3506 |
79,9730 |
84,8206 |
90,5012 |
94,4221 |
105,9881 |
|
66 |
75,4245 |
81,0855 |
85,9649 |
91,6812 |
95,6257 |
107,2579 |
|
67 |
76,4978 |
82,1971 |
87,1081 |
92,8597 |
96,8278 |
108,5256 |
|
68 |
77,5707 |
83,3079 |
88,2502 |
94,0370 |
98,0284 |
109,7913 |
|
69 |
78,6429 |
84,4179 |
89,3912 |
95,2129 |
99,2275 |
111,0551 |
|
70 |
79,7146 |
85,5270 |
90,5312 |
96,3875 |
100,4252 |
112,3169 |
|
71 |
80,7859 |
86,6354 |
91,6702 |
97,5609 |
101,6214 |
113,5769 |
|
72 |
81,8566 |
87,7430 |
92,8083 |
98,7331 |
102,8163 |
114,8351 |
|
73 |
82,9268 |
88,8499 |
93,9453 |
99,9041 |
104,0098 |
116,0915 |
|
74 |
83,9965 |
89,9560 |
95,0815 |
101,0739 |
105,2020 |
117,3462 |
|
75 |
85,0658 |
91,0615 |
96,2167 |
102,2425 |
106,3929 |
118,5991 |
|
76 |
86,1346 |
92,1662 |
97,3510 |
103,4101 |
107,5825 |
119,8503 |
|
77 |
87,2030 |
93,2702 |
98,4844 |
104,5765 |
108,7709 |
121,1000 |
|
78 |
88,2709 |
94,3735 |
99,6169 |
105,7418 |
109,9581 |
122,3480 |
|
79 |
89,3383 |
95,4762 |
100,7486 |
106,9061 |
111,1440 |
123,5944 |
|
80 |
90,4053 |
96,5782 |
101,8795 |
108,0693 |
112,3288 |
124,8392 |
|
81 |
91,4720 |
97,6796 |
103,0095 |
109,2316 |
113,5124 |
126,0826 |
|
82 |
92,5382 |
98,7803 |
104,1387 |
110,3928 |
114,6949 |
127,3244 |
|
83 |
93,6039 |
99,8805 |
105,2672 |
111,5530 |
115,8763 |
128,5648 |
|
84 |
94,6693 |
100,9800 |
106,3948 |
112,7123 |
117,0565 |
129,8037 |
|
85 |
95,7343 |
102,0789 |
107,5217 |
113,8706 |
118,2357 |
131,0412 |
|
86 |
96,7990 |
103,1773 |
108,6479 |
115,0279 |
119,4139 |
132,2773 |
|
87 |
97,8632 |
104,2750 |
109,7733 |
116,1844 |
120,5910 |
133,5121 |
|
88 |
98,9271 |
105,3722 |
110,8980 |
117,3400 |
121,7671 |
134,7455 |
|
89 |
99,9906 |
106,4689 |
112,0220 |
118,4946 |
122,9422 |
135,9776 |
|
90 |
101,0537 |
107,5650 |
113,1453 |
119,6485 |
124,1163 |
137,2084 |
|
91 |
102,1165 |
108,6606 |
114,2679 |
120,8014 |
125,2895 |
138,4379 |
|
92 |
103,1790 |
109,7556 |
115,3898 |
121,9535 |
126,4617 |
139,6661 |
|
93 |
104,2411 |
110,8502 |
116,5110 |
123,1048 |
127,6329 |
140,8931 |
|
94 |
105,3028 |
111,9442 |
117,6317 |
124,2553 |
128,8032 |
142,1189 |
|
95 |
106,3643 |
113,0377 |
118,7516 |
125,4049 |
129,9727 |
143,3435 |
|
96 |
107,4254 |
114,1307 |
119,8709 |
126,5538 |
131,1412 |
144,5670 |
|
97 |
108,4862 |
115,2232 |
120,9896 |
127,7019 |
132,3089 |
145,7892 |
|
98 |
109,5467 |
116,3153 |
122,1077 |
128,8492 |
133,4757 |
147,0104 |
|
99 |
110,6068 |
117,4069 |
123,2252 |
129,9958 |
134,6416 |
148,2304 |
|
100 |
111,6667 |
118,4980 |
124,3421 |
131,1417 |
135,8067 |
149,4493 |
|
110 |
122,2495 |
129,3851 |
135,4802 |
142,5617 |
147,4143 |
161,5807 |
|
120 |
132,8063 |
140,2326 |
146,5674 |
153,9182 |
158,9502 |
173,6174 |
|
130 |
143,3401 |
151,0452 |
157,6099 |
165,2192 |
170,4231 |
185,5710 |
|
140 |
153,8537 |
161,8270 |
168,6130 |
176,4709 |
181,8403 |
197,4508 |
|
150 |
164,3492 |
172,5812 |
179,5806 |
187,6785 |
193,2077 |
209,2646 |
|
160 |
174,8283 |
183,3106 |
190,5165 |
198,8464 |
204,5301 |
221,0190 |
|
170 |
185,2926 |
194,0174 |
201,4234 |
209,9782 |
215,8117 |
232,7194 |
|
180 |
195,7434 |
204,7037 |
212,3039 |
221,0772 |
227,0561 |
244,3705 |
|
190 |
206,1818 |
215,3711 |
223,1602 |
232,1460 |
238,2664 |
255,9763 |
|
200 |
216,6088 |
226,0210 |
233,9943 |
243,1869 |
249,4451 |
267,5405 |
|
210 |
227,0252 |
236,6549 |
244,8076 |
254,2021 |
260,5947 |
279,0661 |
|
220 |
237,4317 |
247,2739 |
255,6018 |
265,1934 |
271,7172 |
290,5558 |
|
230 |
247,8291 |
257,8788 |
266,3781 |
276,1623 |
282,8145 |
302,0120 |
|
240 |
258,2179 |
268,4707 |
277,1376 |
287,1103 |
293,8881 |
313,4369 |
|
250 |
268,5986 |
279,0504 |
287,8815 |
298,0388 |
304,9396 |
324,8324 |
|
260 |
278,9718 |
289,6186 |
298,6106 |
308,9489 |
315,9702 |
336,2003 |
|
270 |
289,3379 |
300,1759 |
309,3258 |
319,8416 |
326,9811 |
347,5422 |
|
280 |
299,6972 |
310,7230 |
320,0278 |
330,7179 |
337,9735 |
358,8595 |
|
290 |
310,0502 |
321,2604 |
330,7174 |
341,5786 |
348,9483 |
370,1534 |
|
300 |
320,3971 |
331,7885 |
341,3951 |
352,4246 |
359,9064 |
381,4252 |
|
350 |
372,0506 |
384,3060 |
394,6258 |
406,4574 |
414,4736 |
437,4883 |
|
400 |
423,5895 |
436,6490 |
447,6325 |
460,2108 |
468,7245 |
493,1318 |
|
450 |
475,0347 |
488,8493 |
500,4562 |
513,7359 |
522,7169 |
548,4324 |
|
500 |
526,4014 |
540,9303 |
553,1268 |
567,0698 |
576,4928 |
603,4460 |
|
550 |
577,7013 |
592,9095 |
605,6668 |
620,2407 |
630,0842 |
658,2147 |
|
600 |
628,9433 |
644,8004 |
658,0936 |
673,2703 |
683,5156 |
712,7712 |
|
650 |
680,1344 |
696,6141 |
710,4211 |
726,1761 |
736,8067 |
767,1415 |
|
700 |
731,2805 |
748,3591 |
762,6607 |
778,9721 |
789,9735 |
821,3468 |
|
750 |
782,3863 |
800,0428 |
814,8215 |
831,6698 |
843,0290 |
875,4044 |
|
800 |
833,4557 |
851,6712 |
866,9114 |
884,2789 |
895,9843 |
929,3289 |
|
850 |
884,4923 |
903,2495 |
918,9369 |
936,8077 |
948,8485 |
983,1326 |
|
900 |
935,4987 |
954,7819 |
970,9036 |
989,2631 |
1001,6296 |
1036,8260 |
|
950 |
986,4775 |
1006,2723 |
1022,8164 |
1041,6512 |
1054,3344 |
1090,4182 |
|
1000 |
1037,4309 |
1057,7239 |
1074,6794 |
1093,9772 |
1106,9690 |
1143,9171 |
3. segédtáblázat: Student-eloszlás kritikus értékei (kétoldali t-próbához) 0,90-0,30 tartományban
|
DF\t |
0,90 |
0,80 |
0,70 |
0,60 |
0,50 |
0,40 |
0,30 |
|---|---|---|---|---|---|---|---|
|
1 |
0,1584 |
0,3249 |
0,5095 |
0,7265 |
1,0000 |
1,3764 |
1,9626 |
|
2 |
0,1421 |
0,2887 |
0,4447 |
0,6172 |
0,8165 |
1,0607 |
1,3862 |
|
3 |
0,1366 |
0,2767 |
0,4242 |
0,5844 |
0,7649 |
0,9785 |
1,2498 |
|
4 |
0,1338 |
0,2707 |
0,4142 |
0,5686 |
0,7407 |
0,9410 |
1,1896 |
|
5 |
0,1322 |
0,2672 |
0,4082 |
0,5594 |
0,7267 |
0,9195 |
1,1558 |
|
6 |
0,1311 |
0,2648 |
0,4043 |
0,5534 |
0,7176 |
0,9057 |
1,1342 |
|
7 |
0,1303 |
0,2632 |
0,4015 |
0,5491 |
0,7111 |
0,8960 |
1,1192 |
|
8 |
0,1297 |
0,2619 |
0,3995 |
0,5459 |
0,7064 |
0,8889 |
1,1081 |
|
9 |
0,1293 |
0,2610 |
0,3979 |
0,5435 |
0,7027 |
0,8834 |
1,0997 |
|
10 |
0,1289 |
0,2602 |
0,3966 |
0,5415 |
0,6998 |
0,8791 |
1,0931 |
|
11 |
0,1286 |
0,2596 |
0,3956 |
0,5399 |
0,6974 |
0,8755 |
1,0877 |
|
12 |
0,1283 |
0,2590 |
0,3947 |
0,5386 |
0,6955 |
0,8726 |
1,0832 |
|
13 |
0,1281 |
0,2586 |
0,3940 |
0,5375 |
0,6938 |
0,8702 |
1,0795 |
|
14 |
0,1280 |
0,2582 |
0,3933 |
0,5366 |
0,6924 |
0,8681 |
1,0763 |
|
15 |
0,1278 |
0,2579 |
0,3928 |
0,5357 |
0,6912 |
0,8662 |
1,0735 |
|
16 |
0,1277 |
0,2576 |
0,3923 |
0,5350 |
0,6901 |
0,8647 |
1,0711 |
|
17 |
0,1276 |
0,2573 |
0,3919 |
0,5344 |
0,6892 |
0,8633 |
1,0690 |
|
18 |
0,1274 |
0,2571 |
0,3915 |
0,5338 |
0,6884 |
0,8620 |
1,0672 |
|
19 |
0,1274 |
0,2569 |
0,3912 |
0,5333 |
0,6876 |
0,8610 |
1,0655 |
|
20 |
0,1273 |
0,2567 |
0,3909 |
0,5329 |
0,6870 |
0,8600 |
1,0640 |
|
21 |
0,1272 |
0,2566 |
0,3906 |
0,5325 |
0,6864 |
0,8591 |
1,0627 |
|
22 |
0,1271 |
0,2564 |
0,3904 |
0,5321 |
0,6858 |
0,8583 |
1,0614 |
|
23 |
0,1271 |
0,2563 |
0,3902 |
0,5317 |
0,6853 |
0,8575 |
1,0603 |
|
24 |
0,1270 |
0,2562 |
0,3900 |
0,5314 |
0,6848 |
0,8569 |
1,0593 |
|
25 |
0,1269 |
0,2561 |
0,3898 |
0,5312 |
0,6844 |
0,8562 |
1,0584 |
|
26 |
0,1269 |
0,2560 |
0,3896 |
0,5309 |
0,6840 |
0,8557 |
1,0575 |
|
27 |
0,1268 |
0,2559 |
0,3894 |
0,5306 |
0,6837 |
0,8551 |
1,0567 |
|
28 |
0,1268 |
0,2558 |
0,3893 |
0,5304 |
0,6834 |
0,8546 |
1,0560 |
|
29 |
0,1268 |
0,2557 |
0,3892 |
0,5302 |
0,6830 |
0,8542 |
1,0553 |
|
30 |
0,1267 |
0,2556 |
0,3890 |
0,5300 |
0,6828 |
0,8538 |
1,0547 |
|
31 |
0,1267 |
0,2555 |
0,3889 |
0,5298 |
0,6825 |
0,8534 |
1,0541 |
|
32 |
0,1267 |
0,2555 |
0,3888 |
0,5297 |
0,6822 |
0,8530 |
1,0535 |
|
33 |
0,1266 |
0,2554 |
0,3887 |
0,5295 |
0,6820 |
0,8526 |
1,0530 |
|
34 |
0,1266 |
0,2553 |
0,3886 |
0,5294 |
0,6818 |
0,8523 |
1,0525 |
|
35 |
0,1266 |
0,2553 |
0,3885 |
0,5292 |
0,6816 |
0,8520 |
1,0520 |
|
36 |
0,1266 |
0,2552 |
0,3884 |
0,5291 |
0,6814 |
0,8517 |
1,0516 |
|
37 |
0,1265 |
0,2552 |
0,3883 |
0,5289 |
0,6812 |
0,8514 |
1,0512 |
|
38 |
0,1265 |
0,2551 |
0,3882 |
0,5288 |
0,6810 |
0,8512 |
1,0508 |
|
39 |
0,1265 |
0,2551 |
0,3882 |
0,5287 |
0,6808 |
0,8509 |
1,0504 |
|
40 |
0,1265 |
0,2550 |
0,3881 |
0,5286 |
0,6807 |
0,8507 |
1,0500 |
|
41 |
0,1264 |
0,2550 |
0,3880 |
0,5285 |
0,6805 |
0,8505 |
1,0497 |
|
42 |
0,1264 |
0,2550 |
0,3880 |
0,5284 |
0,6804 |
0,8503 |
1,0494 |
|
43 |
0,1264 |
0,2549 |
0,3879 |
0,5283 |
0,6802 |
0,8501 |
1,0491 |
|
44 |
0,1264 |
0,2549 |
0,3878 |
0,5282 |
0,6801 |
0,8499 |
1,0488 |
|
45 |
0,1264 |
0,2549 |
0,3878 |
0,5281 |
0,6800 |
0,8497 |
1,0485 |
|
46 |
0,1264 |
0,2548 |
0,3877 |
0,5281 |
0,6799 |
0,8495 |
1,0483 |
|
47 |
0,1263 |
0,2548 |
0,3877 |
0,5280 |
0,6797 |
0,8493 |
1,0480 |
|
48 |
0,1263 |
0,2548 |
0,3876 |
0,5279 |
0,6796 |
0,8492 |
1,0478 |
|
49 |
0,1263 |
0,2547 |
0,3876 |
0,5278 |
0,6795 |
0,8490 |
1,0475 |
|
50 |
0,1263 |
0,2547 |
0,3875 |
0,5278 |
0,6794 |
0,8489 |
1,0473 |
|
51 |
0,1263 |
0,2547 |
0,3875 |
0,5277 |
0,6793 |
0,8487 |
1,0471 |
|
52 |
0,1263 |
0,2546 |
0,3875 |
0,5276 |
0,6792 |
0,8486 |
1,0469 |
|
53 |
0,1263 |
0,2546 |
0,3874 |
0,5276 |
0,6791 |
0,8485 |
1,0467 |
|
54 |
0,1263 |
0,2546 |
0,3874 |
0,5275 |
0,6791 |
0,8483 |
1,0465 |
|
55 |
0,1262 |
0,2546 |
0,3873 |
0,5275 |
0,6790 |
0,8482 |
1,0463 |
|
56 |
0,1262 |
0,2546 |
0,3873 |
0,5274 |
0,6789 |
0,8481 |
1,0461 |
|
57 |
0,1262 |
0,2545 |
0,3873 |
0,5273 |
0,6788 |
0,8480 |
1,0459 |
|
58 |
0,1262 |
0,2545 |
0,3872 |
0,5273 |
0,6787 |
0,8479 |
1,0458 |
|
59 |
0,1262 |
0,2545 |
0,3872 |
0,5272 |
0,6787 |
0,8478 |
1,0456 |
|
60 |
0,1262 |
0,2545 |
0,3872 |
0,5272 |
0,6786 |
0,8477 |
1,0455 |
|
61 |
0,1262 |
0,2545 |
0,3871 |
0,5272 |
0,6785 |
0,8476 |
1,0453 |
|
62 |
0,1262 |
0,2544 |
0,3871 |
0,5271 |
0,6785 |
0,8475 |
1,0452 |
|
63 |
0,1262 |
0,2544 |
0,3871 |
0,5271 |
0,6784 |
0,8474 |
1,0450 |
|
64 |
0,1262 |
0,2544 |
0,3871 |
0,5270 |
0,6783 |
0,8473 |
1,0449 |
|
65 |
0,1262 |
0,2544 |
0,3870 |
0,5270 |
0,6783 |
0,8472 |
1,0448 |
|
66 |
0,1261 |
0,2544 |
0,3870 |
0,5269 |
0,6782 |
0,8471 |
1,0446 |
|
67 |
0,1261 |
0,2544 |
0,3870 |
0,5269 |
0,6782 |
0,8470 |
1,0445 |
|
68 |
0,1261 |
0,2543 |
0,3870 |
0,5269 |
0,6781 |
0,8469 |
1,0444 |
|
69 |
0,1261 |
0,2543 |
0,3869 |
0,5268 |
0,6781 |
0,8469 |
1,0443 |
|
70 |
0,1261 |
0,2543 |
0,3869 |
0,5268 |
0,6780 |
0,8468 |
1,0442 |
|
71 |
0,1261 |
0,2543 |
0,3869 |
0,5268 |
0,6780 |
0,8467 |
1,0441 |
|
72 |
0,1261 |
0,2543 |
0,3869 |
0,5267 |
0,6779 |
0,8466 |
1,0440 |
|
73 |
0,1261 |
0,2543 |
0,3868 |
0,5267 |
0,6779 |
0,8466 |
1,0438 |
|
74 |
0,1261 |
0,2543 |
0,3868 |
0,5267 |
0,6778 |
0,8465 |
1,0437 |
|
75 |
0,1261 |
0,2542 |
0,3868 |
0,5266 |
0,6778 |
0,8464 |
1,0436 |
|
76 |
0,1261 |
0,2542 |
0,3868 |
0,5266 |
0,6777 |
0,8464 |
1,0436 |
|
77 |
0,1261 |
0,2542 |
0,3868 |
0,5266 |
0,6777 |
0,8463 |
1,0435 |
|
78 |
0,1261 |
0,2542 |
0,3867 |
0,5266 |
0,6776 |
0,8463 |
1,0434 |
|
79 |
0,1261 |
0,2542 |
0,3867 |
0,5265 |
0,6776 |
0,8462 |
1,0433 |
|
80 |
0,1261 |
0,2542 |
0,3867 |
0,5265 |
0,6776 |
0,8461 |
1,0432 |
|
81 |
0,1261 |
0,2542 |
0,3867 |
0,5265 |
0,6775 |
0,8461 |
1,0431 |
|
82 |
0,1261 |
0,2542 |
0,3867 |
0,5264 |
0,6775 |
0,8460 |
1,0430 |
|
83 |
0,1260 |
0,2542 |
0,3867 |
0,5264 |
0,6775 |
0,8460 |
1,0429 |
|
84 |
0,1260 |
0,2542 |
0,3866 |
0,5264 |
0,6774 |
0,8459 |
1,0429 |
|
85 |
0,1260 |
0,2541 |
0,3866 |
0,5264 |
0,6774 |
0,8459 |
1,0428 |
|
86 |
0,1260 |
0,2541 |
0,3866 |
0,5263 |
0,6774 |
0,8458 |
1,0427 |
|
87 |
0,1260 |
0,2541 |
0,3866 |
0,5263 |
0,6773 |
0,8458 |
1,0426 |
|
88 |
0,1260 |
0,2541 |
0,3866 |
0,5263 |
0,6773 |
0,8457 |
1,0426 |
|
89 |
0,1260 |
0,2541 |
0,3866 |
0,5263 |
0,6773 |
0,8457 |
1,0425 |
|
90 |
0,1260 |
0,2541 |
0,3866 |
0,5263 |
0,6772 |
0,8456 |
1,0424 |
|
91 |
0,1260 |
0,2541 |
0,3865 |
0,5262 |
0,6772 |
0,8456 |
1,0424 |
|
92 |
0,1260 |
0,2541 |
0,3865 |
0,5262 |
0,6772 |
0,8455 |
1,0423 |
|
93 |
0,1260 |
0,2541 |
0,3865 |
0,5262 |
0,6771 |
0,8455 |
1,0422 |
|
94 |
0,1260 |
0,2541 |
0,3865 |
0,5262 |
0,6771 |
0,8455 |
1,0422 |
|
95 |
0,1260 |
0,2541 |
0,3865 |
0,5262 |
0,6771 |
0,8454 |
1,0421 |
|
96 |
0,1260 |
0,2541 |
0,3865 |
0,5261 |
0,6771 |
0,8454 |
1,0421 |
|
97 |
0,1260 |
0,2540 |
0,3865 |
0,5261 |
0,6770 |
0,8453 |
1,0420 |
|
98 |
0,1260 |
0,2540 |
0,3865 |
0,5261 |
0,6770 |
0,8453 |
1,0419 |
|
99 |
0,1260 |
0,2540 |
0,3864 |
0,5261 |
0,6770 |
0,8453 |
1,0419 |
|
100 |
0,1260 |
0,2540 |
0,3864 |
0,5261 |
0,6770 |
0,8452 |
1,0418 |
|
110 |
0,1260 |
0,2540 |
0,3863 |
0,5259 |
0,6767 |
0,8449 |
1,0413 |
|
120 |
0,1259 |
0,2539 |
0,3862 |
0,5258 |
0,6765 |
0,8446 |
1,0409 |
|
130 |
0,1259 |
0,2539 |
0,3862 |
0,5257 |
0,6764 |
0,8444 |
1,0406 |
|
140 |
0,1259 |
0,2538 |
0,3861 |
0,5256 |
0,6762 |
0,8442 |
1,0403 |
|
150 |
0,1259 |
0,2538 |
0,3861 |
0,5255 |
0,6761 |
0,8440 |
1,0400 |
|
160 |
0,1259 |
0,2538 |
0,3860 |
0,5254 |
0,6760 |
0,8439 |
1,0398 |
|
170 |
0,1258 |
0,2537 |
0,3860 |
0,5254 |
0,6759 |
0,8437 |
1,0396 |
|
180 |
0,1258 |
0,2537 |
0,3859 |
0,5253 |
0,6759 |
0,8436 |
1,0394 |
|
190 |
0,1258 |
0,2537 |
0,3859 |
0,5253 |
0,6758 |
0,8435 |
1,0393 |
|
200 |
0,1258 |
0,2537 |
0,3859 |
0,5252 |
0,6757 |
0,8434 |
1,0391 |
|
210 |
0,1258 |
0,2537 |
0,3858 |
0,5252 |
0,6757 |
0,8433 |
1,0390 |
|
220 |
0,1258 |
0,2537 |
0,3858 |
0,5252 |
0,6756 |
0,8433 |
1,0389 |
|
230 |
0,1258 |
0,2536 |
0,3858 |
0,5251 |
0,6756 |
0,8432 |
1,0388 |
|
240 |
0,1258 |
0,2536 |
0,3858 |
0,5251 |
0,6755 |
0,8431 |
1,0387 |
|
250 |
0,1258 |
0,2536 |
0,3858 |
0,5251 |
0,6755 |
0,8431 |
1,0386 |
|
260 |
0,1258 |
0,2536 |
0,3857 |
0,5250 |
0,6754 |
0,8430 |
1,0385 |
|
270 |
0,1258 |
0,2536 |
0,3857 |
0,5250 |
0,6754 |
0,8430 |
1,0384 |
|
280 |
0,1258 |
0,2536 |
0,3857 |
0,5250 |
0,6754 |
0,8429 |
1,0384 |
|
290 |
0,1258 |
0,2536 |
0,3857 |
0,5250 |
0,6753 |
0,8429 |
1,0383 |
|
300 |
0,1258 |
0,2536 |
0,3857 |
0,5250 |
0,6753 |
0,8428 |
1,0382 |
|
350 |
0,1258 |
0,2535 |
0,3856 |
0,5249 |
0,6752 |
0,8426 |
1,0380 |
|
400 |
0,1257 |
0,2535 |
0,3856 |
0,5248 |
0,6751 |
0,8425 |
1,0378 |
|
450 |
0,1257 |
0,2535 |
0,3856 |
0,5248 |
0,6750 |
0,8424 |
1,0376 |
|
500 |
0,1257 |
0,2535 |
0,3855 |
0,5247 |
0,6750 |
0,8423 |
1,0375 |
|
550 |
0,1257 |
0,2535 |
0,3855 |
0,5247 |
0,6749 |
0,8423 |
1,0374 |
|
600 |
0,1257 |
0,2535 |
0,3855 |
0,5247 |
0,6749 |
0,8422 |
1,0373 |
|
650 |
0,1257 |
0,2535 |
0,3855 |
0,5247 |
0,6749 |
0,8422 |
1,0373 |
|
700 |
0,1257 |
0,2534 |
0,3855 |
0,5246 |
0,6748 |
0,8421 |
1,0372 |
|
750 |
0,1257 |
0,2534 |
0,3855 |
0,5246 |
0,6748 |
0,8421 |
1,0372 |
|
800 |
0,1257 |
0,2534 |
0,3855 |
0,5246 |
0,6748 |
0,8421 |
1,0371 |
|
850 |
0,1257 |
0,2534 |
0,3855 |
0,5246 |
0,6748 |
0,8420 |
1,0371 |
|
900 |
0,1257 |
0,2534 |
0,3854 |
0,5246 |
0,6748 |
0,8420 |
1,0370 |
|
950 |
0,1257 |
0,2534 |
0,3854 |
0,5246 |
0,6747 |
0,8420 |
1,0370 |
|
1000 |
0,1257 |
0,2534 |
0,3854 |
0,5246 |
0,6747 |
0,8420 |
1,0370 |
|
∞ |
0,1257 |
0,2533 |
0,3853 |
0,5244 |
0,6745 |
0,8416 |
1,0364 |
4. segédtáblázat: Student-eloszlás kritikus értékei (kétoldali t-próbához) 0,20-0,001 tartományban
|
DF\t |
0,20 |
0,10 |
0,05 |
0,02 |
0,01 |
0,001 |
|---|---|---|---|---|---|---|
|
1 |
3,0777 |
6,3138 |
12,7062 |
31,8205 |
63,6567 |
636,6192 |
|
2 |
1,8856 |
2,9200 |
4,3027 |
6,9646 |
9,9248 |
31,5991 |
|
3 |
1,6377 |
2,3534 |
3,1824 |
4,5407 |
5,8409 |
12,9240 |
|
4 |
1,5332 |
2,1318 |
2,7764 |
3,7469 |
4,6041 |
8,6103 |
|
5 |
1,4759 |
2,0150 |
2,5706 |
3,3649 |
4,0321 |
6,8688 |
|
6 |
1,4398 |
1,9432 |
2,4469 |
3,1427 |
3,7074 |
5,9588 |
|
7 |
1,4149 |
1,8946 |
2,3646 |
2,9980 |
3,4995 |
5,4079 |
|
8 |
1,3968 |
1,8595 |
2,3060 |
2,8965 |
3,3554 |
5,0413 |
|
9 |
1,3830 |
1,8331 |
2,2622 |
2,8214 |
3,2498 |
4,7809 |
|
10 |
1,3722 |
1,8125 |
2,2281 |
2,7638 |
3,1693 |
4,5869 |
|
11 |
1,3634 |
1,7959 |
2,2010 |
2,7181 |
3,1058 |
4,4370 |
|
12 |
1,3562 |
1,7823 |
2,1788 |
2,6810 |
3,0545 |
4,3178 |
|
13 |
1,3502 |
1,7709 |
2,1604 |
2,6503 |
3,0123 |
4,2208 |
|
14 |
1,3450 |
1,7613 |
2,1448 |
2,6245 |
2,9768 |
4,1405 |
|
15 |
1,3406 |
1,7531 |
2,1314 |
2,6025 |
2,9467 |
4,0728 |
|
16 |
1,3368 |
1,7459 |
2,1199 |
2,5835 |
2,9208 |
4,0150 |
|
17 |
1,3334 |
1,7396 |
2,1098 |
2,5669 |
2,8982 |
3,9651 |
|
18 |
1,3304 |
1,7341 |
2,1009 |
2,5524 |
2,8784 |
3,9216 |
|
19 |
1,3277 |
1,7291 |
2,0930 |
2,5395 |
2,8609 |
3,8834 |
|
20 |
1,3253 |
1,7247 |
2,0860 |
2,5280 |
2,8453 |
3,8495 |
|
21 |
1,3232 |
1,7207 |
2,0796 |
2,5176 |
2,8314 |
3,8193 |
|
22 |
1,3212 |
1,7171 |
2,0739 |
2,5083 |
2,8188 |
3,7921 |
|
23 |
1,3195 |
1,7139 |
2,0687 |
2,4999 |
2,8073 |
3,7676 |
|
24 |
1,3178 |
1,7109 |
2,0639 |
2,4922 |
2,7969 |
3,7454 |
|
25 |
1,3163 |
1,7081 |
2,0595 |
2,4851 |
2,7874 |
3,7251 |
|
26 |
1,3150 |
1,7056 |
2,0555 |
2,4786 |
2,7787 |
3,7066 |
|
27 |
1,3137 |
1,7033 |
2,0518 |
2,4727 |
2,7707 |
3,6896 |
|
28 |
1,3125 |
1,7011 |
2,0484 |
2,4671 |
2,7633 |
3,6739 |
|
29 |
1,3114 |
1,6991 |
2,0452 |
2,4620 |
2,7564 |
3,6594 |
|
30 |
1,3104 |
1,6973 |
2,0423 |
2,4573 |
2,7500 |
3,6460 |
|
31 |
1,3095 |
1,6955 |
2,0395 |
2,4528 |
2,7440 |
3,6335 |
|
32 |
1,3086 |
1,6939 |
2,0369 |
2,4487 |
2,7385 |
3,6218 |
|
33 |
1,3077 |
1,6924 |
2,0345 |
2,4448 |
2,7333 |
3,6109 |
|
34 |
1,3070 |
1,6909 |
2,0322 |
2,4411 |
2,7284 |
3,6007 |
|
35 |
1,3062 |
1,6896 |
2,0301 |
2,4377 |
2,7238 |
3,5911 |
|
36 |
1,3055 |
1,6883 |
2,0281 |
2,4345 |
2,7195 |
3,5821 |
|
37 |
1,3049 |
1,6871 |
2,0262 |
2,4314 |
2,7154 |
3,5737 |
|
38 |
1,3042 |
1,6860 |
2,0244 |
2,4286 |
2,7116 |
3,5657 |
|
39 |
1,3036 |
1,6849 |
2,0227 |
2,4258 |
2,7079 |
3,5581 |
|
40 |
1,3031 |
1,6839 |
2,0211 |
2,4233 |
2,7045 |
3,5510 |
|
41 |
1,3025 |
1,6829 |
2,0195 |
2,4208 |
2,7012 |
3,5442 |
|
42 |
1,3020 |
1,6820 |
2,0181 |
2,4185 |
2,6981 |
3,5377 |
|
43 |
1,3016 |
1,6811 |
2,0167 |
2,4163 |
2,6951 |
3,5316 |
|
44 |
1,3011 |
1,6802 |
2,0154 |
2,4141 |
2,6923 |
3,5258 |
|
45 |
1,3006 |
1,6794 |
2,0141 |
2,4121 |
2,6896 |
3,5203 |
|
46 |
1,3002 |
1,6787 |
2,0129 |
2,4102 |
2,6870 |
3,5150 |
|
47 |
1,2998 |
1,6779 |
2,0117 |
2,4083 |
2,6846 |
3,5099 |
|
48 |
1,2994 |
1,6772 |
2,0106 |
2,4066 |
2,6822 |
3,5051 |
|
49 |
1,2991 |
1,6766 |
2,0096 |
2,4049 |
2,6800 |
3,5004 |
|
50 |
1,2987 |
1,6759 |
2,0086 |
2,4033 |
2,6778 |
3,4960 |
|
51 |
1,2984 |
1,6753 |
2,0076 |
2,4017 |
2,6757 |
3,4918 |
|
52 |
1,2980 |
1,6747 |
2,0066 |
2,4002 |
2,6737 |
3,4877 |
|
53 |
1,2977 |
1,6741 |
2,0057 |
2,3988 |
2,6718 |
3,4838 |
|
54 |
1,2974 |
1,6736 |
2,0049 |
2,3974 |
2,6700 |
3,4800 |
|
55 |
1,2971 |
1,6730 |
2,0040 |
2,3961 |
2,6682 |
3,4764 |
|
56 |
1,2969 |
1,6725 |
2,0032 |
2,3948 |
2,6665 |
3,4729 |
|
57 |
1,2966 |
1,6720 |
2,0025 |
2,3936 |
2,6649 |
3,4696 |
|
58 |
1,2963 |
1,6716 |
2,0017 |
2,3924 |
2,6633 |
3,4663 |
|
59 |
1,2961 |
1,6711 |
2,0010 |
2,3912 |
2,6618 |
3,4632 |
|
60 |
1,2958 |
1,6706 |
2,0003 |
2,3901 |
2,6603 |
3,4602 |
|
61 |
1,2956 |
1,6702 |
1,9996 |
2,3890 |
2,6589 |
3,4573 |
|
62 |
1,2954 |
1,6698 |
1,9990 |
2,3880 |
2,6575 |
3,4545 |
|
63 |
1,2951 |
1,6694 |
1,9983 |
2,3870 |
2,6561 |
3,4518 |
|
64 |
1,2949 |
1,6690 |
1,9977 |
2,3860 |
2,6549 |
3,4491 |
|
65 |
1,2947 |
1,6686 |
1,9971 |
2,3851 |
2,6536 |
3,4466 |
|
66 |
1,2945 |
1,6683 |
1,9966 |
2,3842 |
2,6524 |
3,4441 |
|
67 |
1,2943 |
1,6679 |
1,9960 |
2,3833 |
2,6512 |
3,4417 |
|
68 |
1,2941 |
1,6676 |
1,9955 |
2,3824 |
2,6501 |
3,4394 |
|
69 |
1,2939 |
1,6672 |
1,9949 |
2,3816 |
2,6490 |
3,4372 |
|
70 |
1,2938 |
1,6669 |
1,9944 |
2,3808 |
2,6479 |
3,4350 |
|
71 |
1,2936 |
1,6666 |
1,9939 |
2,3800 |
2,6469 |
3,4329 |
|
72 |
1,2934 |
1,6663 |
1,9935 |
2,3793 |
2,6459 |
3,4308 |
|
73 |
1,2933 |
1,6660 |
1,9930 |
2,3785 |
2,6449 |
3,4289 |
|
74 |
1,2931 |
1,6657 |
1,9925 |
2,3778 |
2,6439 |
3,4269 |
|
75 |
1,2929 |
1,6654 |
1,9921 |
2,3771 |
2,6430 |
3,4250 |
|
76 |
1,2928 |
1,6652 |
1,9917 |
2,3764 |
2,6421 |
3,4232 |
|
77 |
1,2926 |
1,6649 |
1,9913 |
2,3758 |
2,6412 |
3,4214 |
|
78 |
1,2925 |
1,6646 |
1,9908 |
2,3751 |
2,6403 |
3,4197 |
|
79 |
1,2924 |
1,6644 |
1,9905 |
2,3745 |
2,6395 |
3,4180 |
|
80 |
1,2922 |
1,6641 |
1,9901 |
2,3739 |
2,6387 |
3,4163 |
|
81 |
1,2921 |
1,6639 |
1,9897 |
2,3733 |
2,6379 |
3,4147 |
|
82 |
1,2920 |
1,6636 |
1,9893 |
2,3727 |
2,6371 |
3,4132 |
|
83 |
1,2918 |
1,6634 |
1,9890 |
2,3721 |
2,6364 |
3,4116 |
|
84 |
1,2917 |
1,6632 |
1,9886 |
2,3716 |
2,6356 |
3,4102 |
|
85 |
1,2916 |
1,6630 |
1,9883 |
2,3710 |
2,6349 |
3,4087 |
|
86 |
1,2915 |
1,6628 |
1,9879 |
2,3705 |
2,6342 |
3,4073 |
|
87 |
1,2914 |
1,6626 |
1,9876 |
2,3700 |
2,6335 |
3,4059 |
|
88 |
1,2912 |
1,6624 |
1,9873 |
2,3695 |
2,6329 |
3,4045 |
|
89 |
1,2911 |
1,6622 |
1,9870 |
2,3690 |
2,6322 |
3,4032 |
|
90 |
1,2910 |
1,6620 |
1,9867 |
2,3685 |
2,6316 |
3,4019 |
|
91 |
1,2909 |
1,6618 |
1,9864 |
2,3680 |
2,6309 |
3,4007 |
|
92 |
1,2908 |
1,6616 |
1,9861 |
2,3676 |
2,6303 |
3,3994 |
|
93 |
1,2907 |
1,6614 |
1,9858 |
2,3671 |
2,6297 |
3,3982 |
|
94 |
1,2906 |
1,6612 |
1,9855 |
2,3667 |
2,6291 |
3,3971 |
|
95 |
1,2905 |
1,6611 |
1,9853 |
2,3662 |
2,6286 |
3,3959 |
|
96 |
1,2904 |
1,6609 |
1,9850 |
2,3658 |
2,6280 |
3,3948 |
|
97 |
1,2903 |
1,6607 |
1,9847 |
2,3654 |
2,6275 |
3,3937 |
|
98 |
1,2902 |
1,6606 |
1,9845 |
2,3650 |
2,6269 |
3,3926 |
|
99 |
1,2902 |
1,6604 |
1,9842 |
2,3646 |
2,6264 |
3,3915 |
|
100 |
1,2901 |
1,6602 |
1,9840 |
2,3642 |
2,6259 |
3,3905 |
|
110 |
1,2893 |
1,6588 |
1,9818 |
2,3607 |
2,6213 |
3,3812 |
|
120 |
1,2886 |
1,6577 |
1,9799 |
2,3578 |
2,6174 |
3,3735 |
|
130 |
1,2881 |
1,6567 |
1,9784 |
2,3554 |
2,6142 |
3,3669 |
|
140 |
1,2876 |
1,6558 |
1,9771 |
2,3533 |
2,6114 |
3,3614 |
|
150 |
1,2872 |
1,6551 |
1,9759 |
2,3515 |
2,6090 |
3,3566 |
|
160 |
1,2869 |
1,6544 |
1,9749 |
2,3499 |
2,6069 |
3,3524 |
|
170 |
1,2866 |
1,6539 |
1,9740 |
2,3485 |
2,6051 |
3,3487 |
|
180 |
1,2863 |
1,6534 |
1,9732 |
2,3472 |
2,6034 |
3,3454 |
|
190 |
1,2860 |
1,6529 |
1,9725 |
2,3461 |
2,6020 |
3,3425 |
|
200 |
1,2858 |
1,6525 |
1,9719 |
2,3451 |
2,6006 |
3,3398 |
|
210 |
1,2856 |
1,6521 |
1,9713 |
2,3442 |
2,5994 |
3,3375 |
|
220 |
1,2854 |
1,6518 |
1,9708 |
2,3434 |
2,5984 |
3,3353 |
|
230 |
1,2852 |
1,6515 |
1,9703 |
2,3427 |
2,5974 |
3,3333 |
|
240 |
1,2851 |
1,6512 |
1,9699 |
2,3420 |
2,5965 |
3,3315 |
|
250 |
1,2849 |
1,6510 |
1,9695 |
2,3414 |
2,5956 |
3,3299 |
|
260 |
1,2848 |
1,6507 |
1,9691 |
2,3408 |
2,5949 |
3,3283 |
|
270 |
1,2847 |
1,6505 |
1,9688 |
2,3402 |
2,5942 |
3,3269 |
|
280 |
1,2846 |
1,6503 |
1,9685 |
2,3397 |
2,5935 |
3,3256 |
|
290 |
1,2845 |
1,6501 |
1,9682 |
2,3393 |
2,5929 |
3,3244 |
|
300 |
1,2844 |
1,6499 |
1,9679 |
2,3388 |
2,5923 |
3,3233 |
|
350 |
1,2840 |
1,6492 |
1,9668 |
2,3370 |
2,5899 |
3,3185 |
|
400 |
1,2837 |
1,6487 |
1,9659 |
2,3357 |
2,5882 |
3,3150 |
|
450 |
1,2834 |
1,6482 |
1,9652 |
2,3347 |
2,5868 |
3,3123 |
|
500 |
1,2832 |
1,6479 |
1,9647 |
2,3338 |
2,5857 |
3,3101 |
|
550 |
1,2831 |
1,6476 |
1,9643 |
2,3331 |
2,5848 |
3,3083 |
|
600 |
1,2830 |
1,6474 |
1,9639 |
2,3326 |
2,5840 |
3,3068 |
|
650 |
1,2829 |
1,6472 |
1,9636 |
2,3321 |
2,5834 |
3,3056 |
|
700 |
1,2828 |
1,6470 |
1,9634 |
2,3317 |
2,5829 |
3,3045 |
|
750 |
1,2827 |
1,6469 |
1,9631 |
2,3313 |
2,5824 |
3,3035 |
|
800 |
1,2826 |
1,6468 |
1,9629 |
2,3310 |
2,5820 |
3,3027 |
|
850 |
1,2825 |
1,6466 |
1,9628 |
2,3307 |
2,5816 |
3,3020 |
|
900 |
1,2825 |
1,6465 |
1,9626 |
2,3305 |
2,5813 |
3,3014 |
|
950 |
1,2824 |
1,6465 |
1,9625 |
2,3303 |
2,5810 |
3,3008 |
|
1000 |
1,2824 |
1,6464 |
1,9623 |
2,3301 |
2,5808 |
3,3003 |
|
∞ |
1,2816 |
1,6449 |
1,9600 |
2,3263 |
2,5758 |
3,2905 |
5. segédtáblázat: Standard normális eloszlás
Használati példa: Ha a Z értéke 0,83, akkor az eloszlási értéket a 0,8x sorában és a 0,03 oszlopában találjuk meg (értéke 0,7967).
|
Z\x |
0,00 |
0,01 |
0,02 |
0,03 |
0,04 |
0,05 |
0,06 |
0,07 |
0,08 |
0,09 |
|---|---|---|---|---|---|---|---|---|---|---|
|
0,0x |
0,5000 |
0,5040 |
0,5080 |
0,5120 |
0,5160 |
0,5199 |
0,5239 |
0,5279 |
0,5319 |
0,5359 |
|
0,1x |
0,5398 |
0,5438 |
0,5478 |
0,5517 |
0,5557 |
0,5596 |
0,5636 |
0,5675 |
0,5714 |
0,5753 |
|
0,2x |
0,5793 |
0,5832 |
0,5871 |
0,5910 |
0,5948 |
0,5987 |
0,6026 |
0,6064 |
0,6103 |
0,6141 |
|
0,3x |
0,6179 |
0,6217 |
0,6255 |
0,6293 |
0,6331 |
0,6368 |
0,6406 |
0,6443 |
0,6480 |
0,6517 |
|
0,4x |
0,6554 |
0,6591 |
0,6628 |
0,6664 |
0,6700 |
0,6736 |
0,6772 |
0,6808 |
0,6844 |
0,6879 |
|
0,5x |
0,6915 |
0,6950 |
0,6985 |
0,7019 |
0,7054 |
0,7088 |
0,7123 |
0,7157 |
0,7190 |
0,7224 |
|
0,6x |
0,7257 |
0,7291 |
0,7324 |
0,7357 |
0,7389 |
0,7422 |
0,7454 |
0,7486 |
0,7517 |
0,7549 |
|
0,7x |
0,7580 |
0,7611 |
0,7642 |
0,7673 |
0,7704 |
0,7734 |
0,7764 |
0,7794 |
0,7823 |
0,7852 |
|
0,8x |
0,7881 |
0,7910 |
0,7939 |
0,7967 |
0,7995 |
0,8023 |
0,8051 |
0,8078 |
0,8106 |
0,8133 |
|
0,9x |
0,8159 |
0,8186 |
0,8212 |
0,8238 |
0,8264 |
0,8289 |
0,8315 |
0,8340 |
0,8365 |
0,8389 |
|
1,0x |
0,8413 |
0,8438 |
0,8461 |
0,8485 |
0,8508 |
0,8531 |
0,8554 |
0,8577 |
0,8599 |
0,8621 |
|
1,1x |
0,8643 |
0,8665 |
0,8686 |
0,8708 |
0,8729 |
0,8749 |
0,8770 |
0,8790 |
0,8810 |
0,8830 |
|
1,2x |
0,8849 |
0,8869 |
0,8888 |
0,8907 |
0,8925 |
0,8944 |
0,8962 |
0,8980 |
0,8997 |
0,9015 |
|
1,3x |
0,9032 |
0,9049 |
0,9066 |
0,9082 |
0,9099 |
0,9115 |
0,9131 |
0,9147 |
0,9162 |
0,9177 |
|
1,4x |
0,9192 |
0,9207 |
0,9222 |
0,9236 |
0,9251 |
0,9265 |
0,9279 |
0,9292 |
0,9306 |
0,9319 |
|
1,5x |
0,9332 |
0,9345 |
0,9357 |
0,9370 |
0,9382 |
0,9394 |
0,9406 |
0,9418 |
0,9429 |
0,9441 |
|
1,6x |
0,9452 |
0,9463 |
0,9474 |
0,9484 |
0,9495 |
0,9505 |
0,9515 |
0,9525 |
0,9535 |
0,9545 |
|
1,7x |
0,9554 |
0,9564 |
0,9573 |
0,9582 |
0,9591 |
0,9599 |
0,9608 |
0,9616 |
0,9625 |
0,9633 |
|
1,8x |
0,9641 |
0,9649 |
0,9656 |
0,9664 |
0,9671 |
0,9678 |
0,9686 |
0,9693 |
0,9699 |
0,9706 |
|
1,9x |
0,9713 |
0,9719 |
0,9726 |
0,9732 |
0,9738 |
0,9744 |
0,9750 |
0,9756 |
0,9761 |
0,9767 |
|
2,0x |
0,9772 |
0,9778 |
0,9783 |
0,9788 |
0,9793 |
0,9798 |
0,9803 |
0,9808 |
0,9812 |
0,9817 |
|
2,1x |
0,9821 |
0,9826 |
0,9830 |
0,9834 |
0,9838 |
0,9842 |
0,9846 |
0,9850 |
0,9854 |
0,9857 |
|
2,2x |
0,9861 |
0,9864 |
0,9868 |
0,9871 |
0,9875 |
0,9878 |
0,9881 |
0,9884 |
0,9887 |
0,9890 |
|
2,3x |
0,9893 |
0,9896 |
0,9898 |
0,9901 |
0,9904 |
0,9906 |
0,9909 |
0,9911 |
0,9913 |
0,9916 |
|
2,4x |
0,9918 |
0,9920 |
0,9922 |
0,9925 |
0,9927 |
0,9929 |
0,9931 |
0,9932 |
0,9934 |
0,9936 |
|
2,5x |
0,9938 |
0,9940 |
0,9941 |
0,9943 |
0,9945 |
0,9946 |
0,9948 |
0,9949 |
0,9951 |
0,9952 |
|
2,6x |
0,9953 |
0,9955 |
0,9956 |
0,9957 |
0,9959 |
0,9960 |
0,9961 |
0,9962 |
0,9963 |
0,9964 |
|
2,7x |
0,9965 |
0,9966 |
0,9967 |
0,9968 |
0,9969 |
0,9970 |
0,9971 |
0,9972 |
0,9973 |
0,9974 |
|
2,8x |
0,9974 |
0,9975 |
0,9976 |
0,9977 |
0,9977 |
0,9978 |
0,9979 |
0,9979 |
0,9980 |
0,9981 |
|
2,9x |
0,9981 |
0,9982 |
0,9982 |
0,9983 |
0,9984 |
0,9984 |
0,9985 |
0,9985 |
0,9986 |
0,9986 |
|
3,0x |
0,9987 |
0,9987 |
0,9987 |
0,9988 |
0,9988 |
0,9989 |
0,9989 |
0,9989 |
0,9990 |
0,9990 |
|
3,1x |
0,9990 |
0,9991 |
0,9991 |
0,9991 |
0,9992 |
0,9992 |
0,9992 |
0,9992 |
0,9993 |
0,9993 |
|
3,2x |
0,9993 |
0,9993 |
0,9994 |
0,9994 |
0,9994 |
0,9994 |
0,9994 |
0,9995 |
0,9995 |
0,9995 |
|
3,3x |
0,9995 |
0,9995 |
0,9995 |
0,9996 |
0,9996 |
0,9996 |
0,9996 |
0,9996 |
0,9996 |
0,9997 |
|
3,4x |
0,9997 |
0,9997 |
0,9997 |
0,9997 |
0,9997 |
0,9997 |
0,9997 |
0,9997 |
0,9997 |
0,9998 |
|
3,5x |
0,9998 |
0,9998 |
0,9998 |
0,9998 |
0,9998 |
0,9998 |
0,9998 |
0,9998 |
0,9998 |
0,9998 |
|
3,6x |
0,9998 |
0,9998 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
|
3,7x |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
|
3,8x |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
|
3,9x |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |